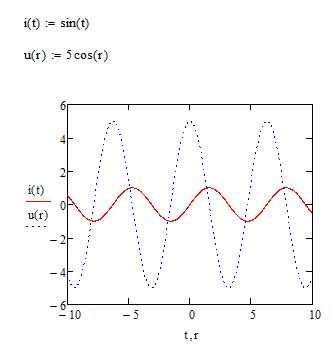
Для анализа данных и визуализации результатов в Mathcad часто используется метод сглаживания графиков, позволяющий убрать шум и повысить точность представления информации. Одним из наиболее популярных подходов является использование метода скользящего среднего или полиномиальных функций для построения более гладких кривых. Этот процесс существенно упрощает восприятие данных, особенно при работе с экспериментальными измерениями, где часто присутствует случайный шум.
Основным инструментом для сглаживания в Mathcad является функция Smooth, которая позволяет применять различные алгоритмы для обработки исходных данных. Для начала необходимо задать исходные данные, которые могут быть представлены в виде массива чисел. Затем, с помощью параметров функции, можно настроить степень сглаживания, чтобы получить желаемый результат. Важно помнить, что слишком сильное сглаживание может скрыть важные детали данных, поэтому необходимо тщательно выбирать параметры.
Для построения сглаженного графика в Mathcad, достаточно выполнить несколько простых шагов. Сначала вводятся данные, например, в виде таблицы. После этого применяется функция сглаживания, например, Smooth(x, window_size), где x – это массив данных, а window_size – размер окна для скользящего среднего. Результатом будет сглаженная версия графика, которая значительно улучшит видимость трендов и паттернов в данных.
Одним из важных аспектов является выбор подходящего типа сглаживания в зависимости от характера данных. Например, для временных рядов идеально подходит метод скользящего среднего, тогда как для обработки функции, имеющей сильные колебания, более подходящими будут полиномиальные методы сглаживания. Правильный выбор метода помогает сохранить ключевые особенности данных, при этом устраняя ненужные флуктуации.
Подготовка исходных данных для сглаживания в Mathcad
Для успешного сглаживания данных в Mathcad, прежде всего, необходимо корректно подготовить исходные данные. Это поможет избежать ошибок при применении математических методов и ускорит процесс анализа. Основные шаги подготовки следующие:
- Очистка данных от выбросов и шумов: Прежде чем приступать к сглаживанию, важно проверить данные на наличие выбросов и аномальных значений, которые могут искажать результаты. Для этого следует использовать методы детекции аномальных точек, такие как межквартильный размах или стандартное отклонение.
- Преобразование данных в подходящий формат: В Mathcad важно, чтобы данные были представлены в виде вектора или массива. Если исходные данные находятся в текстовом формате, их следует конвертировать в числовой массив. Для этого можно воспользоваться встроенными функциями импорта.
- Обработка пропущенных значений: Пропуски данных необходимо либо заполнить (например, методом линейной интерполяции), либо исключить из анализа. Mathcad предоставляет функции для интерполяции и экстраполяции данных, что позволяет восполнить пропуски без искажения статистических характеристик.
- Нормализация и стандартизация данных: Если данные имеют разные масштабы, их следует нормализовать или стандартизировать, чтобы сглаживание не привело к неправильным результатам. Например, для приведения данных к единому масштабу можно использовать метод Min-Max или Z-преобразование.
- Определение необходимой частоты данных: Для сглаживания с помощью фильтрации или других методов важно, чтобы данные имели равномерные интервалы. Если исходные данные собраны с переменной частотой, их следует интерполировать или преобразовать в равномерные интервалы, чтобы применяемая методика сглаживания была корректной.
- Выбор подходящего метода сглаживания: На этапе подготовки необходимо решить, какой метод сглаживания будет использоваться: скользящая средняя, полиномиальная регрессия или другие. Этот выбор зависит от характеристик данных и требований к точности результата. Для каждого метода важны специфические особенности данных, такие как их распределение и наличие тренда.
Правильная подготовка данных существенно повышает точность сглаживания и позволяет получить более надежные результаты в Mathcad.
Выбор метода сглаживания: moving average или spline
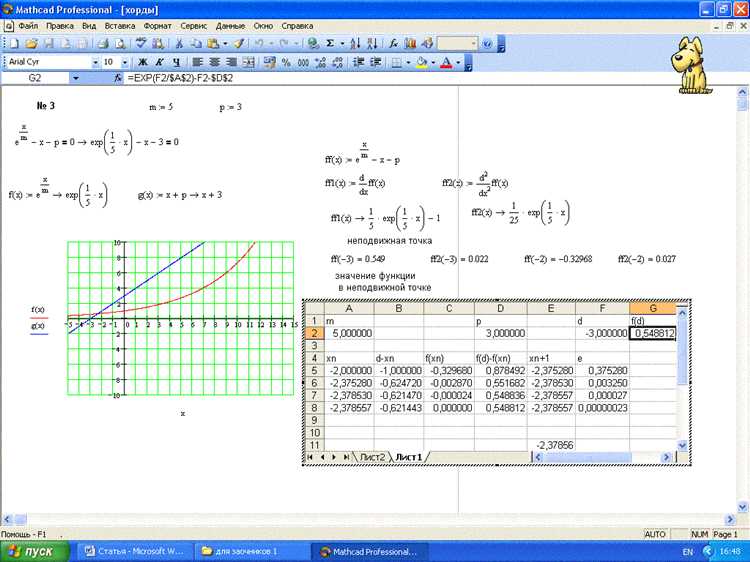
При необходимости сгладить данные для визуализации или анализа, часто используются два метода: скользящее среднее (moving average) и сплайн-интерполяция (spline). Каждый из них имеет свои особенности, подходящие для различных типов данных и задач.
Скользящее среднее подходит для данных с высокой степенью шума, где важно минимизировать влияние отдельных выбросов. Этот метод заменяет каждое значение в ряду средним значением в пределах окна, что эффективно нивелирует случайные колебания. Скользящее среднее можно настроить через выбор размера окна. Малые окна быстрее реагируют на изменения, но могут не сглаживать более крупные колебания. Большие окна, в свою очередь, сглаживают данные сильнее, но могут скрывать быстрые изменения в тренде.
Основное ограничение метода moving average – его способность только к линейному сглаживанию. Если данные содержат сложные, нелинейные закономерности или резкие изменения, скользящее среднее может не адекватно отобразить эти особенности.
Сплайн-интерполяция предоставляет более гибкое и точное сглаживание, создавая непрерывную кривую, которая проходит через все исходные точки данных. Сплайн отлично подходит для данных, где требуется более сложная форма сглаживания, особенно если наблюдаются резкие переходы или нелинейные тренды. Сплайны могут быть как гладкими, так и иметь ограничения по степени гладкости (например, кубические сплайны).
Однако, в отличие от moving average, сплайны могут приводить к переобучению, если модель чрезмерно точно подстраивается под данные. Это особенно актуально в случае с малым количеством точек или нестабильными данными, где сплайн может идеально проходить через все точки, но при этом отражать шум, а не реальную тенденцию.
При выборе между moving average и сплайном важно учитывать структуру и характер данных. Если данные подвержены резким колебаниям и шуму, и при этом сохраняется тенденция, moving average будет оптимальным вариантом. Если же требуется учитывать более сложные, нелинейные тренды с плавными переходами, стоит выбрать сплайн, при этом важно избегать переобучения, регулируя параметры модели.
Настройка параметров сглаживания для точных результатов
В Mathcad для эффективного сглаживания данных необходимо учитывать несколько ключевых параметров, влияющих на точность и корректность получаемых результатов. Правильная настройка этих параметров позволяет получить графики с четкими и адекватными представлениями, избегая искажений или потери важной информации.
Основными параметрами сглаживания являются:
- Метод сглаживания: В Mathcad доступно несколько типов методов, таких как линейное, полиномиальное или сплайн-сглаживание. Каждый метод имеет свои особенности, которые должны соответствовать характеру данных. Для простых данных, где изменения плавные, достаточно линейного метода. Для более сложных кривых лучше использовать полиномиальные или сплайн-методы.
- Параметр порядка полинома: Для полиномиального сглаживания важно правильно выбрать порядок полинома. Высокие порядки могут привести к переобучению модели, в то время как слишком низкие – не обеспечат нужного уровня точности. Оптимальный порядок зависит от характера данных, но обычно не превышает 3-4 степени.
- Число точек для сглаживания: Чем больше точек данных используется для сглаживания, тем более гладким будет результат. Однако слишком большое количество точек может замедлить вычисления и привести к излишнему сглаживанию, теряя детали в данных. Рекомендуется использовать от 5 до 10 точек для каждого интервала данных.
- Параметр регуляции: Регуляция сглаживания помогает контролировать степень сглаживания, предотвращая потерю важных данных. Это особенно важно при использовании сплайн-сглаживания, где неправильный выбор параметра может привести к недооценке или переоценке колебаний в данных.
Кроме того, необходимо обратить внимание на:
- Предобработка данных: Убедитесь, что данные не содержат выбросов и шумов, которые могут негативно повлиять на точность сглаживания. Применение фильтрации или нормализации перед процессом сглаживания может улучшить результаты.
- Точность расчетов: Важно настроить параметры точности в Mathcad. Для более точных результатов стоит увеличить число знаков после запятой в расчетах, особенно если данные чувствительны к мелким изменениям.
- Визуализация: Оцените полученный график, используя различные уровни сглаживания, чтобы понять, как изменяется поведение кривой при разных настройках. Это поможет выбрать оптимальные параметры для дальнейшей работы.
При настройке параметров сглаживания следует всегда учитывать баланс между точностью и эффективностью вычислений. Экспериментирование с разными настройками позволяет найти оптимальное решение, соответствующее требованиям задачи.
Использование встроенных функций Mathcad для сглаживания
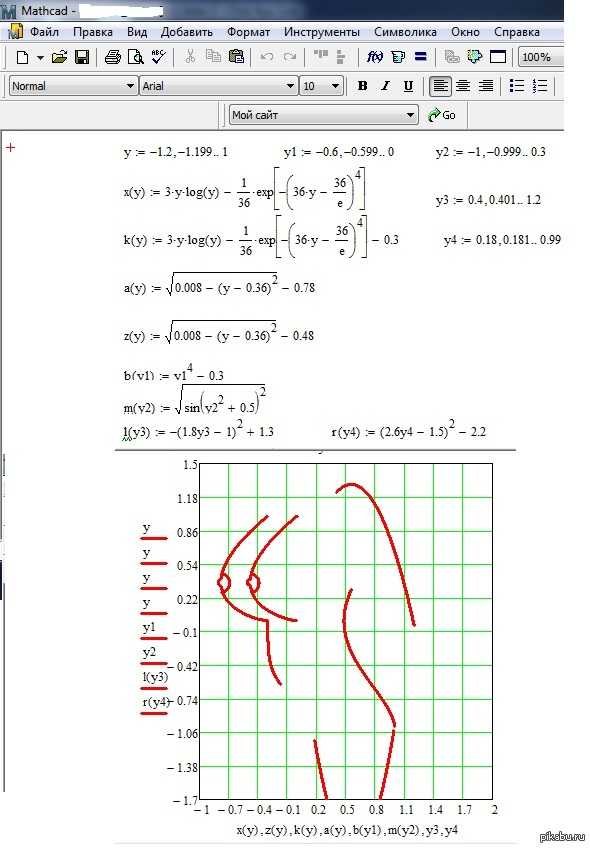
В Mathcad для сглаживания данных можно использовать несколько встроенных функций, которые позволяют эффективно устранять шум и извлекать значимые тренды. Основные методы сглаживания включают фильтрацию, скользящее среднее и методы интерполяции.
Для сглаживания временных рядов или других данных часто используется функция smooth. Эта функция выполняет сглаживание данных с использованием скользящего среднего или других фильтров, таких как гауссово или экспоненциальное сглаживание. Формат вызова функции:
y := smooth(x, n)Здесь x – исходные данные, а n – количество точек в окне скользящего среднего. Чем больше значение n, тем более сглаженным будет результат. Однако стоит учитывать, что слишком большое значение может привести к потерям в деталях данных.
Для выполнения сглаживания с помощью экспоненциального фильтра используется функция expSmooth. Этот метод позволяет сглаживать данные, при этом он сохраняет большую часть информации о тенденциях, а не только локальных колебаниях.
y := expSmooth(x, alpha)Параметр alpha в данном случае задает коэффициент сглаживания, который определяет степень влияния прошлых значений на текущее. Чем больше значение alpha, тем сильнее сглаживание.
Для более сложных случаев, когда требуется использование методов интерполяции, можно применять функцию interpolate. Она подходит для сглаживания данных, когда между точками имеется пробел, и необходимо создать гладкую кривую, проходящую через эти точки.
y := interpolate(x, y, xi)Здесь xi – это набор точек, для которых нужно вычислить значения функции. Эта функция применяется при необходимости сглаживания дискретных данных с интерполяцией между точками, что полезно при работе с нерегулярными данными.
Для продвинутого сглаживания можно использовать методы полиномиальной регрессии или фильтра Калмана, однако они требуют более глубокого понимания математической теории и точных настроек. Mathcad предоставляет гибкие возможности для реализации этих методов через создание пользовательских функций и использование встроенных инструментов оптимизации.
Определение оптимальных значений параметров сглаживания
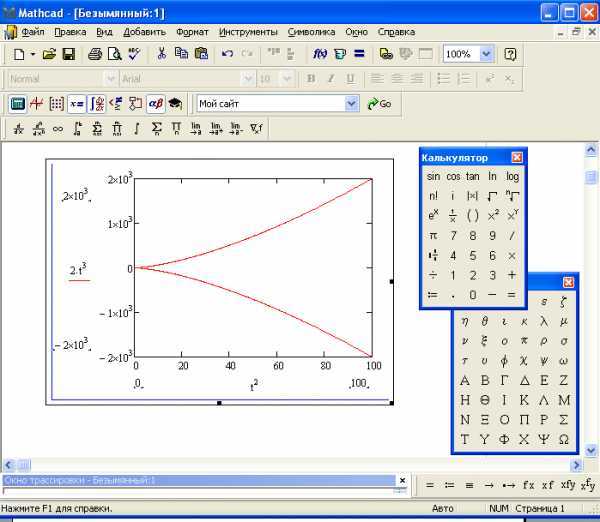
Оптимальные значения параметров сглаживания в Mathcad зависят от типа и характеристик исходных данных, а также от целей анализа. В первую очередь важно выбрать подходящий метод сглаживания, исходя из природы шума и искомых зависимостей.
Для сглаживания данных часто используют методы скользящего среднего, экспоненциального сглаживания и полиномиальных интерполяций. В каждом случае ключевым параметром является «параметр сглаживания», который контролирует степень устранения шума при сохранении тенденций в данных.
Для метода скользящего среднего оптимальным значением параметра считается длина окна, которая должна быть достаточно большой, чтобы охватывать основные колебания, но не настолько большой, чтобы размывать важные детали. Рекомендуемая длина окна может быть выбрана с помощью критерия минимизации ошибки прогноза на тестовой выборке или анализа частотных характеристик исходных данных.
При применении экспоненциального сглаживания ключевым параметром является коэффициент сглаживания α (от 0 до 1). Меньшие значения α дают более плавные графики, но могут терять детали, в то время как большие значения α сохраняют более точную информацию, но могут усиливать шум. Оптимальное значение α можно подобрать методом проб и ошибок или с помощью оценки ошибки на данных из разных временных периодов.
Для полиномиальных методов сглаживания выбор порядка полинома также критичен. Слишком высокий порядок полинома может привести к переобучению модели, тогда как слишком низкий – не уловит основные тенденции. Рекомендуется начинать с полинома второй степени и постепенно увеличивать порядок, сравнивая качество сглаживания на кросс-валидации.
Для более сложных данных с сильными колебаниями полезным инструментом является использование комбинированных методов сглаживания, например, комбинированного экспоненциального и полиномиального сглаживания, что позволяет учитывать как локальные, так и глобальные тенденции.
Определение оптимального параметра также требует учета контекста анализа. Например, если задача состоит в поиске трендов, то сглаживание должно быть настроено таким образом, чтобы минимизировать отклонения от общей тенденции. Если же цель состоит в выявлении закономерностей в малых колебаниях данных, то сглаживание должно быть более агрессивным, чтобы уменьшить влияние крупных флуктуаций.
Построение графика после применения сглаживания
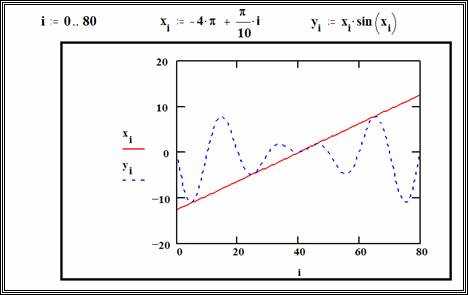
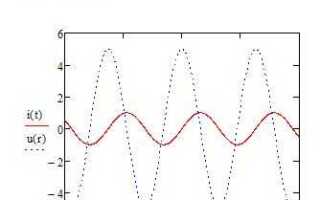
После применения метода сглаживания к данным важно построить график, который наглядно демонстрирует улучшения в точности отображения. Применение сглаживания в Mathcad позволяет уменьшить влияние шума и выделить основные тенденции в наборе данных. Для этого необходимо учитывать, какой метод сглаживания был использован, и какой тип графика будет наиболее информативным для анализа.
Одним из популярных методов сглаживания является скользящее среднее. После его применения следует построить график, отображающий как исходные, так и сглаженные данные. В Mathcad это можно сделать с помощью функции «plot» или «graph», указав два ряда данных: исходные и сглаженные значения. Для корректного отображения на графике нужно убедиться, что шкала оси Y подходит для всех значений, включая сглаженные. В противном случае график может дать искаженное восприятие результата.
Для оценки эффективности сглаживания рекомендуется использовать график с наложением двух кривых: исходной и сглаженной. Это позволит наглядно увидеть, насколько сглаживание уменьшило колебания и шум в данных. При этом следует настроить прозрачность линий или использовать разные стили линий для лучшего визуального разделения данных.
Другим методом, который часто используется для сглаживания данных, является полиномиальная регрессия. В Mathcad для построения такого графика можно использовать функции «polyfit» и «plot». Результат полиномиальной регрессии обычно показывает более гладкую кривую, чем скользящее среднее. Это особенно полезно при анализе данных с более сложными зависимостями.
Для повышения точности визуализации можно применить дополнительные настройки, такие как увеличение разрешения графика и точности осей. Важно, чтобы на графике было видно, как сглаживание влияет на исходные данные и в какой мере оно помогает устранить выбросы. Подбирая параметры сглаживания, следует помнить, что слишком сильное сглаживание может привести к потере важных деталей в данных.
Таким образом, построение графика после применения сглаживания в Mathcad требует внимания к деталям и правильной настройке параметров отображения. Важно не только получить сглаженный график, но и правильно интерпретировать результаты для дальнейшего анализа.
Анализ полученного графика и проверка точности сглаживания
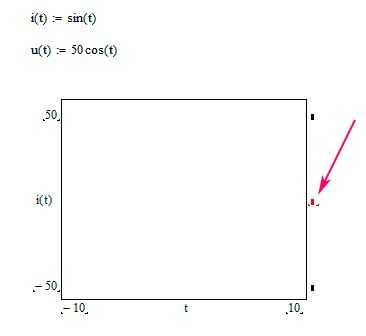
После применения методов сглаживания для уменьшения колебаний исходных данных важно провести анализ полученного графика и оценить точность выполненного сглаживания. Это необходимо для того, чтобы убедиться, что график адекватно отражает тенденции, не теряя значимой информации и не искажая данные.
Первым шагом является визуальная проверка. На графике должно быть четко видно, что сглаженная линия плавно следует за основными колебаниями, не выделяя отдельных выбросов и резких изменений. Однако важно, чтобы сглаживание не выровняло все колебания, уничтожив необходимые флуктуации, которые могут быть значимыми для анализа. Оцените, как выглядит исходная линия в сравнении с обработанной: сглаженная линия должна быть менее «шершавой», но при этом не вытянутой или чрезмерно сглаженной.
Далее, для количественной оценки точности сглаживания необходимо рассчитать ошибку между исходными и сглаженными значениями. Одним из распространенных способов является вычисление среднего квадратичного отклонения (СКО) между исходными данными и результатами сглаживания. Меньшее значение СКО свидетельствует о более точном сглаживании, однако важно учитывать, что минимизация ошибки может привести к потере деталей данных. Оцените это значение в контексте конкретной задачи, чтобы понимать, насколько допустима ошибка в рамках анализа.
Кроме того, полезным инструментом является анализ производных сглаженной функции. В зависимости от задачи можно проверить, насколько сглаженная кривая сохраняет важные изменения в наклоне и амплитуде. Резкие изменения производной, даже если они невелики, могут указывать на потерю информации при сглаживании. В таких случаях рекомендуется корректировать параметры сглаживания или применять более сложные методы фильтрации.
Если задача требует точной передачи данных, можно использовать несколько методов сглаживания, чтобы сравнить результаты. Например, использование сглаживания методом скользящего среднего и метода экспоненциального сглаживания позволит выявить возможные недостатки каждого из методов. Параметры сглаживания (например, окно в методе скользящего среднего) должны быть выбраны так, чтобы минимизировать потери данных при сохранении общей тенденции.
Наконец, не стоит забывать о возможности переноса сглаживания на другие участки данных. Точность сглаживания должна быть проверена не только для основного графика, но и для всех значений, использующих эту функцию в дальнейшем. Анализ возможных ошибок в других частях графика или в процессе интерполяции помогает обеспечить высокое качество сглаживания на всем интервале данных.
Вопрос-ответ:
Как в Mathcad построить сглаженный график для данных?
Для построения сглаженного графика в Mathcad необходимо воспользоваться функцией сглаживания данных, например, с использованием метода скользящего среднего или полиномиального сглаживания. Вначале нужно создать массив данных, затем применить функцию, которая будет вычислять сглаживание по выбранному методу. После этого эти данные можно визуализировать с помощью стандартных инструментов построения графиков, таких как график «Plot». Важно, чтобы перед этим данные были корректно подготовлены: очищены от выбросов и подготовлены к сглаживанию.
Какой метод сглаживания лучше использовать для графика в Mathcad?
Выбор метода сглаживания зависит от типа данных и задачи. Один из популярных методов — это скользящее среднее, который подходит для временных рядов, где важно минимизировать влияние случайных колебаний. В других случаях можно использовать полиномиальное сглаживание, которое обеспечивает более плавный переход между точками и позволяет лучше учитывать тренды данных. Метод сглаживания следует выбирать в зависимости от требуемой точности и характера данных, с которыми работаете.
Можно ли в Mathcad сглаживать графики с учетом определённых точек данных?
Да, в Mathcad можно сглаживать графики с учетом определенных точек данных. Для этого можно использовать функции, которые позволяют вручную задавать параметры сглаживания, например, количество соседних точек для скользящего среднего. Также можно использовать более сложные методы, такие как сплайны или полиномы, которые позволяют более гибко подходить к сглаживанию с учетом заданных условий. Важно при этом правильно настроить параметры, чтобы не потерять важную информацию о данных.
Как визуализировать сглаженные данные в Mathcad?
После того как данные были сглажены, для их визуализации в Mathcad можно использовать инструмент построения графиков, такой как «Plot». Для этого нужно создать массив сглаженных данных и передать его в команду построения графика. Можно добавить различные элементы, например, линии или точки для отображения исходных и сглаженных значений на одном графике. Также возможно настроить стили линий и маркеров, чтобы лучше различать данные и сглаженные значения.