Как сделать сопряженное число в mathcad

Сопряжённое комплексное число для выражения вида a + bi определяется как a — bi. В Mathcad для выполнения этой операции не предусмотрена отдельная встроенная функция, однако можно реализовать построение сопряжённого числа вручную с использованием базовых средств языка.

Для начала необходимо задать переменную, содержащую комплексное число. Например, z := 3 + 4i. Mathcad автоматически воспринимает i как мнимую единицу. Чтобы получить сопряжённое число, воспользуйтесь выражением conj(z) := Re(z) — Im(z)·i. Таким образом, создаётся функция conj, возвращающая нужное значение для любого комплексного аргумента.

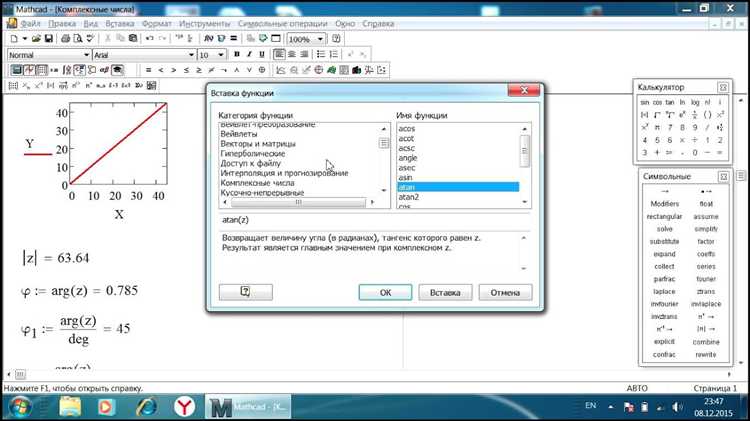
При построении графика сопряжённого числа рекомендуется использовать координатную плоскость с осями действительных и мнимых значений. Mathcad позволяет визуализировать точки с помощью XY Plot, где по оси x откладывается Re(z), а по оси y – Im(z). Для сопряжённого числа знак мнимой части инвертируется, что отражается в симметрии графика относительно действительной оси.

Практическое применение сопряжённого числа в Mathcad особенно важно при выполнении операций с комплексными матрицами и решении уравнений в электротехнике. Правильное определение и визуализация сопряжения позволяет избежать ошибок при комплексных преобразованиях и упрощает интерпретацию результатов.

Как ввести комплексное число в Mathcad вручную

Для ввода комплексного числа в Mathcad используйте стандартную форму a + b*i, где a – действительная часть, b – мнимая, а i – мнимая единица. Символ i вводится автоматически как мнимая единица при условии, что переменная с таким именем не определена ранее.

Если введено выражение 3 + 4i, Mathcad интерпретирует его как комплексное число с действительной частью 3 и мнимой 4. Чтобы избежать конфликтов, не переопределяйте i вручную, иначе выражения перестанут интерпретироваться как комплексные.

Также допустим формат complex(a, b), где a – действительная часть, b – мнимая. Пример: complex(2, -5) создаёт число 2 - 5i.

Все вычисления с такими числами производятся автоматически: Mathcad корректно определяет модуль, аргумент и выполняет арифметику без дополнительных настроек.

Использование встроенной функции conj для получения сопряжённого

В Mathcad для получения сопряжённого комплексного числа применяется функция conj(z), где z – переменная или выражение комплексного типа. Результатом будет число с тем же модулем и противоположным знаком мнимой части.

Пример: пусть z := 3 + 4i. Вызов conj(z) вернёт 3 − 4i. Функция применяется напрямую в строке вычислений без необходимости подключения дополнительных библиотек.

Функция conj корректно работает с элементами вектора или матрицы. Например, при применении conj к вектору V := [1 + i, 2 − 3i], результатом будет [1 − i, 2 + 3i].

Функция поддерживает вложенные выражения: conj(a + b·i + conj(c − d·i)) корректно вычисляется с учётом всех уровней вложенности. Это позволяет использовать conj в формулах без необходимости предварительного разложения выражений на части.

При работе с массивами важно помнить, что conj применяется поэлементно. Это удобно для обработки комплексных сигналов или коэффициентов в численных задачах.

Для проверки корректности результата рекомендуется использовать real и imag – встроенные функции для выделения действительной и мнимой частей соответственно.

Работа с сопряжёнными числами в матрицах

В Mathcad сопряжённые комплексные числа корректно обрабатываются и в скалярной, и в матричной форме. Для получения сопряжённой матрицы используется встроенная функция conj(), применяемая к каждому элементу массива.

• Чтобы создать матрицу с комплексными элементами, задайте её напрямую, например: A := [[1 + 2i, 3 - i][4i, 5]].
• Примените функцию conj(A) для получения сопряжённой матрицы. Mathcad автоматически выполнит сопряжение каждого элемента.
• Для векторно-матричных операций с сопряжёнными элементами убедитесь, что используются совместимые функции. Например, conj(transpose(A)) возвращает эрмитово сопряжённую матрицу.
• При работе с комплексными матрицами важно учитывать порядок умножения. В Mathcad выражение conj(A) * A не эквивалентно A * conj(A), если A – не эрмитова матрица.

Если требуется автоматическая генерация сопряжённой матрицы при вводе данных, используйте вложенные определения. Например:

A := [[a + bi, c - di][e + fi, g]]
Ac := conj(A)

Для численного анализа, таких как поиск собственных значений, Mathcad учитывает комплексную природу элементов. Функция eigvec(conj(A)) возвращает собственные векторы сопряжённой матрицы.

• Сравнение матриц с комплексными элементами должно выполняться с учётом допустимой погрешности: norm(A - conj(B)) < ε.
• Для символьной обработки сопряжённых матриц используйте оператор simplify в сочетании с conj(), если требуется аналитическое упрощение.

Проверка результата: сравнение числа и его сопряжённого

В Mathcad сравнение комплексного числа и его сопряжённого осуществляется через анализ вещественной и мнимой частей. Пусть задано число z := 3 + 4·i. Сопряжённое к нему записывается как conj(z).

Для проверки корректности:

• Вычислите z и conj(z) в отдельной строке.
• Вычислите сумму z + conj(z) – результатом должно быть число без мнимой части (в примере: 6).
• Вычислите разность z − conj(z) – результатом должно быть чисто мнимое число (в примере: 8·i).
• Вычислите произведение z·conj(z) – результат всегда вещественный: |z|² (в примере: 25).

Для визуального подтверждения можно использовать команду rectangular(z) и rectangular(conj(z)), чтобы убедиться, что мнимые части отличаются знаком, а вещественные совпадают.

Дополнительная проверка: функция Im(z) + Im(conj(z)) всегда должна возвращать ноль, а Re(z) − Re(conj(z)) – тоже ноль.

Построение графика сопряжённого числа на комплексной плоскости

Для визуализации сопряжённого числа в Mathcad необходимо использовать декартову форму комплексного числа и функции отображения точек на координатной плоскости. Сопряжённое число имеет ту же действительную часть, но мнимую с противоположным знаком.

1. Задайте исходное комплексное число, например:
   z := 3 + 4i
2. Найдите сопряжённое число с помощью функции conj:
   z_conj := conj(z)
3. Создайте векторы для отображения точек на плоскости:
   X := [Re(z), Re(z_conj)]
Y := [Im(z), Im(z_conj)]
4. Постройте график с использованием функции XYPlot:
   • Добавьте первую точку (Re(z), Im(z)) – оригинальное число
   • Добавьте вторую точку (Re(z_conj), Im(z_conj)) – сопряжённое
5. Настройте отображение:
   • Отключите соединение точек, чтобы они отображались отдельно
   • Добавьте подписи с помощью надписей или стрелок
   • Убедитесь, что ось X – действительная, ось Y – мнимая

Такой подход позволяет чётко отобразить симметрию комплексного числа и его сопряжённого относительно оси действительных чисел.

Создание пользовательской функции для сопряжения чисел

В Mathcad встроенной функции для получения сопряжённого комплексного числа нет, однако можно создать пользовательскую функцию. Откройте рабочий лист и введите следующее определение:

conj(z) := Re(z) - i·Im(z)

Эта функция принимает аргумент z, извлекает его действительную часть с помощью Re(z) и мнимую часть через Im(z), после чего формирует новое число с противоположной мнимой частью. Символ i обозначает мнимую единицу и должен быть включён в настройки документа (если он отключён, активируйте через «Calculations» → «Unit System»).

Для проверки работы функции введите, например:

z := 3 + 4·i

conj(z) =

Mathcad выведет результат 3 - 4·i, что подтверждает корректную реализацию. Убедитесь, что используете точку в качестве десятичного разделителя, если региональные настройки требуют этого. Пользовательская функция работает как с переменными, так и с выражениями, содержащими комплексные числа.

Применение сопряжённых чисел в инженерных расчётах

Сопряжённые числа активно применяются при анализе электрических цепей переменного тока. В частности, в комплексной форме представления импедансов используется сопряжение для нахождения мощности и построения диаграмм мощности. Например, полная мощность S выражается как произведение напряжения U на сопряжение тока I*: S = U · I*. Это позволяет отделить активную и реактивную составляющие, что критически важно при проектировании энергоустановок.

В механике сплошных сред сопряжённые числа применяются при решении задач колебаний и волновых процессов. При анализе гармонических колебаний амплитудно-фазовый метод оперирует комплексными переменными, где сопряжение требуется для вычисления действительных физических величин, таких как среднеквадратичное значение колебаний и фазовые сдвиги.

В строительной механике сопряжённые числа используются при расчётах динамического отклика конструкций на периодические нагрузки. При решении уравнений с комплексными коэффициентами сопряжение обеспечивает получение физически корректных решений и интерпретацию амплитудных характеристик в устойчивых режимах.

В Mathcad сопряжённое число вызывается через встроенную функцию conj(z), где z – комплексное выражение. Это особенно полезно при символьных вычислениях и моделировании цепей, в которых важна точность фазового анализа. Использование conj() совместно с функциями real(z) и imag(z) позволяет эффективно извлекать реальные параметры из комплексных моделей.

Частые ошибки при работе с сопряжёнными числами в Mathcad

1. Использование стандартной функции conj без указания формата числа

Mathcad корректно вычисляет сопряжённое число только для переменных, объявленных как комплексные. Если число представлено в виде строки или результатом численного выражения без мнимой части, функция conj(z) возвращает исходное значение без изменений. Перед применением conj убедитесь, что переменная содержит мнимую часть или явно приведена к комплексному типу, например: z := 3 + 0·i.

2. Ошибки при операциях с матрицами комплексных чисел

При применении conj к матрице Mathcad выполняет сопряжение поэлементно. Однако при этом нельзя путать сопряжение с эрмитовым транспонированием. Для получения эрмитово-сопряжённой матрицы необходимо вручную объединить транспонирование и сопряжение: conj(transpose(A)), а не просто conj(A).

3. Неверное использование чисел с плавающей точкой

Из-за особенностей численной точности Mathcad может неправильно интерпретировать очень малую мнимую часть как ноль. Например, z := 5 + 1·10⁻¹⁴·i может быть обработано как действительное число, и conj(z) вернёт тот же результат. Чтобы избежать этого, используйте мнимую часть, заведомо отличимую от нуля или работайте в символьном режиме.

4. Отсутствие явного указания комплексного формата в пользовательских функциях

При создании собственных функций, возвращающих комплексные значения, Mathcad по умолчанию может интерпретировать их как действительные. Это приводит к тому, что сопряжение таких результатов не работает. Объявляйте переменные с использованием i внутри функции или предварительно задавайте Re(z) и Im(z) явно.

5. Игнорирование различий между символьным и численным режимами

Функция conj в символьном режиме может давать выражение в общем виде, например conj(a + b·i) → a – b·i. В численном режиме тот же ввод даст конкретное значение. Пользователи часто забывают переключать режимы в зависимости от задачи, что ведёт к непредсказуемым результатам.

Вопрос-ответ: