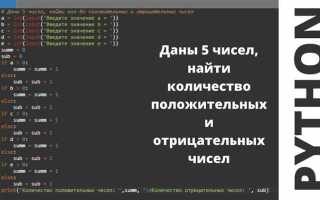Как вести число в python

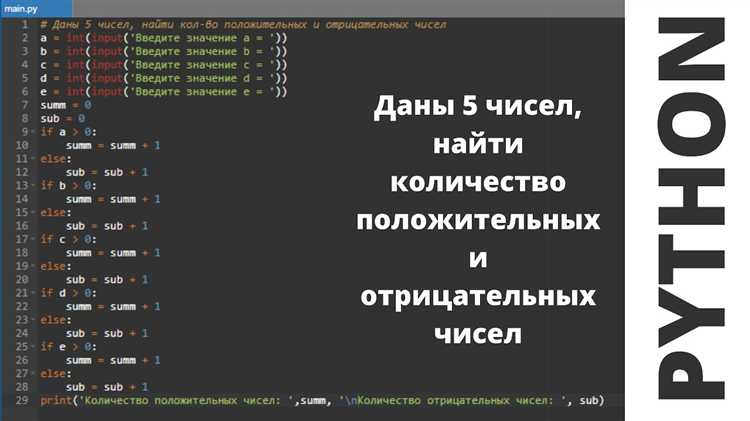
Python предоставляет несколько типов данных для работы с числами, каждый из которых подходит для решения разных задач. Основными типами чисел являются целые числа (int) и числа с плавающей запятой (float). Преимущество Python в том, что он автоматически выбирает подходящий тип для операций, но важно понимать особенности их использования.

Целые числа в Python могут быть любыми, от небольших до очень больших. Нет фиксированного ограничения на размер чисел, поскольку Python автоматически использует память в зависимости от величины числа. Однако при работе с большими числами стоит учитывать, что их обработка может занимать больше времени, что повлияет на производительность.

Для работы с числами с плавающей запятой Python использует стандарт IEEE 754. Это позволяет точно представлять числа с десятичными дробями, но из-за ограничений двоичного представления могут возникать погрешности при операциях с ними. Например, выражение 0.1 + 0.2 может дать результат, который не совсем ожидаем – 0.30000000000000004 вместо точного значения 0.3.

Особое внимание стоит уделить работе с операциями над числами. В Python присутствуют все стандартные арифметические операции, а также функции для извлечения квадратного корня, нахождения факториала и работы с тригонометрическими функциями. Для округления чисел можно использовать встроенную функцию round(), которая позволяет точно контролировать количество знаков после запятой.

Для более сложных операций и работы с большими числами полезно использовать дополнительные библиотеки, такие как math и decimal. math предоставляет множество математических функций, а decimal – более точную работу с числами, что важно при финансовых расчетах.

Преобразование типов данных в числа

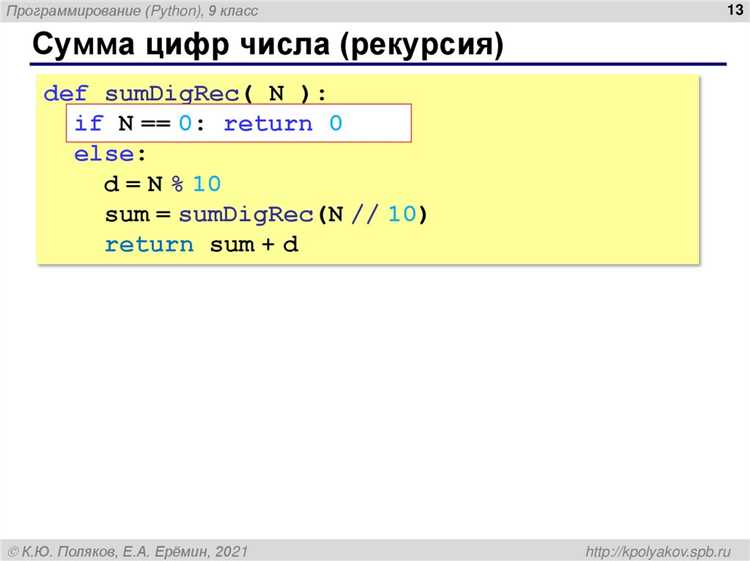
В Python преобразование типов данных в числа осуществляется с помощью встроенных функций, таких как int(), float() и complex(). Эти функции позволяют преобразовывать строки, логические значения и другие типы в числовые типы данных.

int() используется для преобразования строки или другого типа в целое число. Если строка содержит некорректные символы, будет вызвана ошибка. Например, int("123") возвращает целое число 123, а int("123.45") вызовет ошибку.

Для преобразования строки с десятичной точкой в число с плавающей запятой используется float(). Эта функция также может принимать строковые значения с экспоненциальной записью. Например, float("123.45") вернёт число 123.45, а float("1e3") даст 1000.0.

Если нужно преобразовать строку или число в комплексное число, используйте complex(). Эта функция принимает строку в формате «a+bj» или два числа для мнимой и действительной части. Пример: complex("3+4j") вернёт комплексное число 3+4j.

Также важно помнить, что при преобразовании строки в число Python игнорирует пробелы в начале и конце строки, но возникнет ошибка, если строка будет содержать недопустимые символы. Например, int(" 123 ") успешно вернёт 123, а int("123abc") вызовет исключение.

Примеры использования:

# Преобразование строки в целое число
x = int("100")
# Преобразование строки в число с плавающей запятой
y = float("3.14159")
# Преобразование строки в комплексное число
z = complex("5+6j")

Важно помнить, что при неправильном преобразовании данных Python выбросит исключение ValueError, которое нужно обрабатывать с помощью конструкции try-except.

Пример обработки ошибки:

try:
num = int("123abc")
except ValueError:
print("Ошибка преобразования строки в число")

Работа с целыми числами и операциями над ними

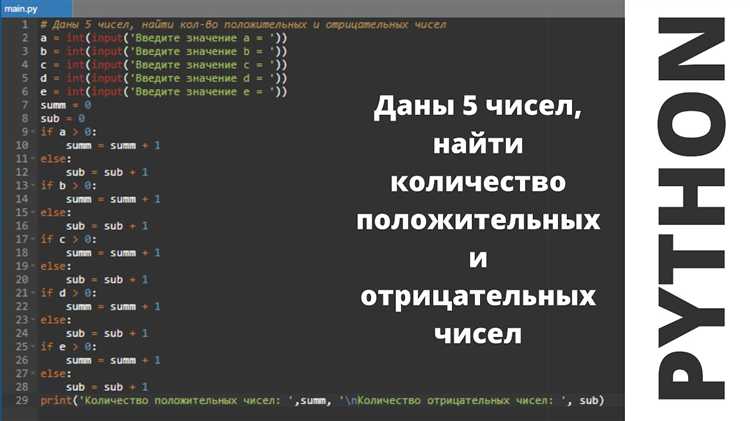
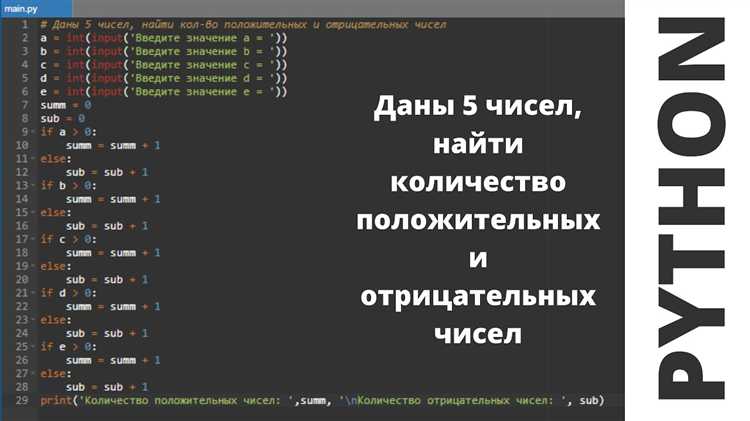
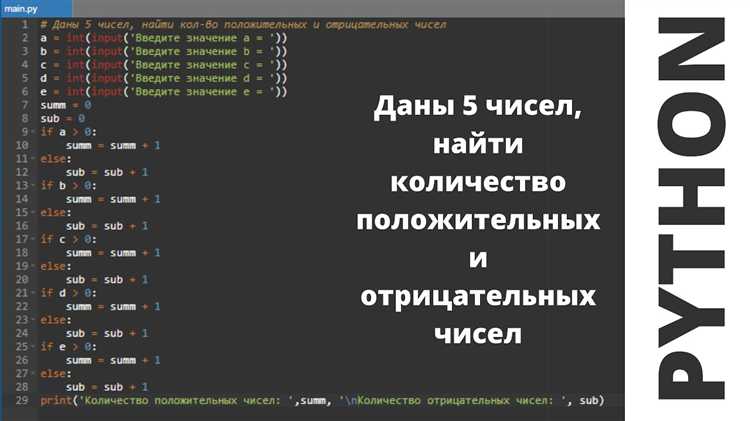
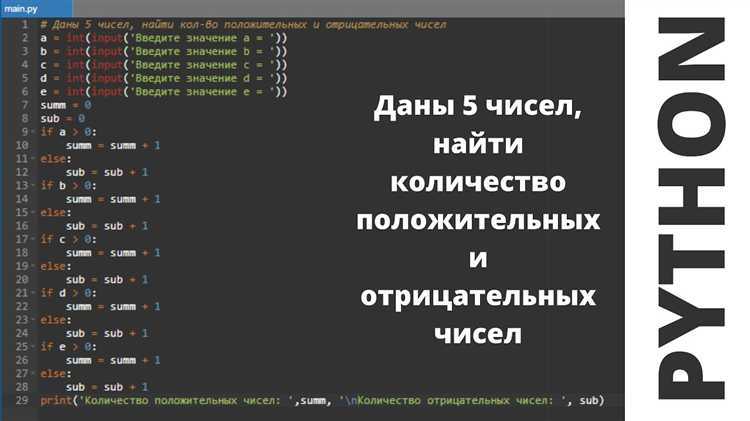
Основные операции:

Сложение: Оператор + используется для сложения двух чисел. Например, 5 + 3 даст результат 8.
Вычитание: Оператор - позволяет вычесть одно число из другого. Например, 5 - 3 даст 2.
Умножение: Оператор * используется для умножения. Пример: 4 * 3 возвращает 12.
Деление: Оператор / делит одно число на другое, возвращая результат с плавающей запятой (например, 5 / 2 даст 2.5).
Целочисленное деление: Оператор // выполняет деление с округлением вниз до ближайшего целого числа. Например, 5 // 2 вернёт 2.
Остаток от деления: Оператор % возвращает остаток от деления. Например, 5 % 2 даст 1.
Возведение в степень: Оператор используется для возведения числа в степень. Пример: 3 2 даст 9.

Особенности работы с целыми числами:

Неограниченные целые числа: В Python целые числа не ограничены размером, что отличает его от многих других языков. Вы можете работать с числами, которые значительно превышают пределы 32-битных или 64-битных целых чисел.
Округление: При операциях деления важно помнить, что оператор / всегда возвращает число с плавающей запятой, а // всегда округляет результат вниз. Это поведение важно учитывать, когда точность не является приоритетом.
Модификация значений: Для выполнения операций на месте можно использовать операторы +=, -=, *=, /= и другие, что позволяет изменять переменную без необходимости присваивания результата в отдельную переменную.

Рекомендации:

Используйте целочисленное деление // и остаток от деления % для задач, где важно работать именно с целыми числами.
Для повышения читаемости кода не смешивайте операции с разными типами данных, например, целые и вещественные числа, особенно при делении.
Если требуется точный результат, учитывайте поведение оператора / и избегайте использования // в вычислениях, где точность важна.

Числа с плавающей точкой: создание и точность вычислений

Числа с плавающей точкой в Python представляют собой числа, которые могут иметь дробную часть, и хранятся в формате с плавающей точкой (float). Они применяются, когда требуется работать с величинами, которые не могут быть выражены целыми числами, например, для расчетов в математике или физике.

Для создания числа с плавающей точкой достаточно указать его в виде числа с десятичной дробью. Например, 3.14 или 0.001 являются числами с плавающей точкой. Также возможна запись с использованием экспоненциальной формы: 1.5e2 будет равно 150.0.

Погрешности при работе с числами с плавающей точкой часто возникают из-за того, что такие числа представляют собой приближенные значения в двоичной системе. Например, число 0.1 в двоичной системе невозможно точно представить, поэтому при попытке вывести результат вычислений с участием 0.1, можно заметить небольшие погрешности, например, результат 0.1 + 0.2 может быть равен 0.30000000000000004, а не 0.3.

Чтобы избежать таких погрешностей при сравнении чисел, рекомендуется использовать функцию math.isclose(), которая позволяет задать допустимую погрешность для сравнения двух чисел. Например:

import math
math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-9)

Это гарантирует корректное сравнение чисел с плавающей точкой при заданной точности. Однако при больших вычислениях важно помнить, что накопление ошибок в процессе обработки данных может приводить к значительным отклонениям в результате, особенно при использовании большого количества операций с плавающей точкой.

Округление чисел с плавающей точкой может быть важным для получения точных результатов. Python предоставляет функцию round() для округления чисел до заданного количества знаков после запятой. Например:

round(3.14159, 2)

Это округлит число 3.14159 до двух знаков после запятой, получив 3.14. Однако стоит помнить, что функция round() использует «ближайшее четное» правило округления, что может привести к неожиданным результатам в некоторых случаях.

Для работы с более точными расчетами, особенно в финансовых приложениях, стоит обратить внимание на модуль decimal, который позволяет работать с числами произвольной точности, избегая погрешностей стандартных типов данных. Например, использование decimal.Decimal позволяет более точно работать с числами, такими как денежные суммы, в отличие от float:

from decimal import Decimal
d1 = Decimal('0.1')
d2 = Decimal('0.2')
result = d1 + d2

В отличие от обычных чисел с плавающей точкой, при работе с Decimal результат сложения будет точно равен 0.3, без лишних погрешностей.

Также важно помнить, что Python использует 64-битный формат для представления чисел с плавающей точкой, что ограничивает точность хранения и вычислений. В случае необходимости работы с числами более высокой точности, можно использовать библиотеки, такие как mpmath, которые поддерживают произвольную точность.

Использование встроенных функций для работы с числами

Python предоставляет набор встроенных функций, которые позволяют эффективно работать с числами, независимо от их типа – целые числа или числа с плавающей точкой. Рассмотрим наиболее полезные из них.

abs() – возвращает абсолютное значение числа. Эта функция полезна, если необходимо работать с величинами, не учитывая знак. Например, abs(-7) вернет 7, а abs(3) оставит число без изменений.

round() – используется для округления числа до заданного количества знаков после запятой. Например, round(3.14159, 2) вернет 3.14. Если количество знаков не указано, по умолчанию округление происходит до целого числа.

pow() – возводит число в степень. Синтаксис pow(x, y) эквивалентен выражению x y. Например, pow(2, 3) вернет 8. Также pow поддерживает третий аргумент для вычисления остатка от деления: pow(x, y, z) вычисляет (x y) % z.

divmod() – возвращает кортеж, содержащий частное и остаток от деления двух чисел. Например, divmod(7, 3) вернет (2, 1), где 2 – это частное, а 1 – остаток.

min() и max() – функции для нахождения минимального и максимального значения среди переданных чисел. Пример: min(1, 5, 3) вернет 1, а max(1, 5, 3) вернет 5. Эти функции также могут работать с последовательностями, такими как списки или кортежи.

sum() – вычисляет сумму элементов итерируемого объекта. Например, sum([1, 2, 3, 4]) вернет 10. Это удобный способ для быстрого подсчета суммы элементов в списке или другом iterable.

int() и float() – преобразуют строки или другие числовые значения в целые числа или числа с плавающей точкой соответственно. Пример: int(«123») вернет 123, а float(«3.14») вернет 3.14. Они полезны для работы с вводимыми данными или при необходимости изменить тип числа.

isinstance() – проверяет, является ли объект экземпляром указанного типа. Например, isinstance(10, int) вернет True, а isinstance(10.5, int) – False. Эта функция полезна при валидации данных в программах, работающих с числами.

Эти функции упрощают работу с числами и позволяют выполнять задачи более компактно и эффективно. Использование встроенных инструментов Python сокращает время на разработку и повышает читаемость кода.

Математические библиотеки Python для сложных вычислений

Python предлагает ряд мощных библиотек для выполнения сложных математических вычислений. Каждая из них предназначена для специфических задач и позволяет решать проблемы, от линейной алгебры до численных методов и статистики.

Некоторые из наиболее популярных и эффективных библиотек для выполнения сложных вычислений включают:

NumPy – основная библиотека для работы с массивами и матрицами данных. Она предоставляет широкий спектр математических функций, таких как линейная алгебра, статистика, операции с многомерными массивами и трансформации. Это базовый инструмент для научных вычислений в Python.
SciPy – расширение для NumPy, которое включает более сложные методы численных вычислений, такие как оптимизация, интеграция, решение дифференциальных уравнений и интерполяция данных. Используется для задач, требующих продвинутых численных методов.
SymPy – библиотека для символьных вычислений, позволяющая работать с выражениями в аналитической форме. Она поддерживает операции с алгебраическими выражениями, вычисление производных, интегралов и решение уравнений.
Matplotlib – инструмент для визуализации данных. Эта библиотека полезна для построения графиков, диаграмм и визуальных представлений результатов сложных вычислений. Она широко используется в научных исследованиях и анализе данных.
Pandas – библиотека для работы с табличными данными, которая может быть полезна при анализе больших массивов числовых и текстовых данных. Она позволяет легко манипулировать данными, агрегировать их и выполнять статистические операции.
PyTorch и TensorFlow – библиотеки для машинного обучения и работы с нейронными сетями, которые включают встроенные функции для выполнения сложных математических операций на больших объемах данных, таких как градиентный спуск и многомерные вычисления.

Для применения этих библиотек в реальных задачах важно знать их особенности:

NumPy подходит для быстрого выполнения арифметических операций с массивами. Он оптимизирован для работы с большими данными, что делает его основным выбором для математики и науки.
SciPy является отличным выбором для выполнения научных расчетов, требующих специфических методов, таких как решение уравнений или нахождение интегралов. Если NumPy не хватает возможностей, SciPy предлагает более высокоуровневые функции.
SymPy не используется для численных расчетов, но идеально подходит для аналитических задач, когда нужно получать точные символьные результаты или проводить упрощение математических выражений.

Использование этих библиотек вместе позволяет эффективно решать разнообразные математические задачи в Python. Например, вы можете использовать NumPy для манипуляции данными, SciPy для численных расчетов, а SymPy для точных аналитических решений. Matplotlib поможет визуализировать результаты, а Pandas упростит обработку данных перед применением математических методов.

Каждая из этих библиотек имеет свою нишу в экосистеме Python и предоставляет пользователям необходимые инструменты для решения сложных вычислительных задач.

Обработка ошибок при работе с числами и делением на ноль

При работе с числами в Python часто встречаются ошибки, особенно когда речь идет о делении на ноль. Попытка выполнить деление на ноль вызывает исключение типа ZeroDivisionError, что прерывает выполнение программы. Для предотвращения таких ситуаций важно грамотно обрабатывать возможные ошибки.

Основной подход к обработке ошибок – использование блока try-except. Он позволяет перехватывать исключения и выполнять альтернативные действия. Например, для безопасного деления можно использовать следующий код:

try:
result = numerator / denominator
except ZeroDivisionError:
result = "Деление на ноль невозможно"

В данном примере, если переменная denominator равна нулю, программа не завершится с ошибкой, а вместо этого выведет сообщение о невозможности деления на ноль.

Если предполагается, что возможны другие ошибки, связанные с типами данных (например, деление строк или объектов), можно добавить дополнительные исключения:

try:
result = numerator / denominator
except ZeroDivisionError:
result = "Деление на ноль невозможно"
except TypeError:
result = "Некорректные данные для деления"

Кроме этого, важно учитывать типы чисел. Python автоматически приводит целые числа к типу с плавающей запятой при выполнении операций с ними, но это может вызвать неожиданное поведение. Чтобы избежать ошибок, связанных с неожиданными типами данных, можно использовать явные проверки типа:

if isinstance(numerator, (int, float)) and isinstance(denominator, (int, float)):
try:
result = numerator / denominator
except ZeroDivisionError:
result = "Деление на ноль невозможно"
else:
result = "Ожидались числа для деления"

Этот код предотвратит попытку деления, если один из операндов не является числом, что сделает программу более устойчивой.

Для более сложных операций с числами рекомендуется учитывать возможные исключения при работе с библиотеками, такими как math, которые могут генерировать ошибки при выполнении математических операций. Например, попытка вычисления квадратного корня из отрицательного числа через math.sqrt() вызовет исключение ValueError. Для таких ситуаций также стоит использовать обработку ошибок:

import math
try:
result = math.sqrt(-1)
except ValueError:
result = "Невозможно вычислить квадратный корень из отрицательного числа"

Грамотная обработка ошибок при работе с числами позволяет избежать сбоев и делает код более надежным и предсказуемым. Важно понимать, что каждый тип ошибок требует своего подхода, и использование конструкций try-except помогает правильно реагировать на возможные проблемы.

Вопрос-ответ:

Как в Python работать с числами с плавающей точкой?

В Python числа с плавающей точкой представлены типом данных `float`. Чтобы работать с такими числами, достаточно просто использовать их в выражениях, например: `3.14 + 2.5` или `float(3)`. Операции с числами с плавающей точкой включают сложение, вычитание, умножение и деление. Также важно помнить, что при использовании чисел с плавающей точкой могут возникать проблемы с точностью, связанные с особенностями представления этих чисел в памяти компьютера. Чтобы избежать ошибок округления, можно использовать модуль `decimal` для более точных вычислений.

Что такое целые числа в Python и как их использовать?

Целые числа в Python — это числа без десятичной части, они имеют тип данных `int`. Такие числа используются для выполнения различных математических операций, таких как сложение, вычитание, умножение и деление. Пример: `5 + 3`, `12 — 4`, `7 * 2`. Целые числа могут быть как положительными, так и отрицательными. Важно, что Python автоматически поддерживает очень большие и очень маленькие числа (в пределах возможностей системы). Вы можете использовать такие числа без опасений по поводу переполнения, что отличает Python от многих других языков программирования.

Как округлить число в Python?

Для округления чисел в Python используется функция `round()`. Она принимает два аргумента: число, которое нужно округлить, и количество знаков после запятой. Пример: `round(3.14159, 2)` вернет `3.14`. Если второй аргумент не указан, то число округляется до ближайшего целого. Однако важно учитывать, что функция `round()` округляет числа «по правилам», что может не всегда дать ожидаемый результат при работе с числами с плавающей точкой из-за особенностей их представления. Для более точного контроля над округлением можно использовать модуль `decimal`.

Какие существуют типы чисел в Python?

В Python существует несколько типов чисел, которые можно использовать в различных ситуациях. Основные типы чисел — это целые числа (`int`) и числа с плавающей точкой (`float`). Также в Python есть тип `complex`, который используется для представления комплексных чисел. Пример целого числа: `5`, пример числа с плавающей точкой: `3.14`, пример комплексного числа: `3 + 4j`. Каждый из этих типов имеет свои особенности и области применения. Например, `int` используется для работы с целыми числами, а `float` — для расчетов, требующих точности с дробной частью, таких как научные вычисления. Комплексные числа полезны в математике и инженерии для представления величин, которые имеют как реальную, так и мнимую часть.