
Задача нахождения количества делителей числа встречается в различных областях программирования, от анализа чисел до криптографии. В Python существует несколько методов для решения этой задачи, и выбор оптимального подхода зависит от размера числа и специфики задачи. В этой статье мы рассмотрим наиболее эффективные способы нахождения количества делителей числа с помощью Python.
Основной принцип заключается в том, что для числа n делители – это все числа, на которые n делится без остатка. Простое решение – пройтись по всем числам от 1 до n и проверить, делится ли n на каждое из них. Однако этот метод неэффективен для больших чисел, так как его сложность составляет O(n).
Более эффективным способом является использование свойства парных делителей. Для каждого делителя числа d существует второй, равный n/d. Это позволяет ограничить проверку до чисел, не превышающих квадратный корень из n, что значительно ускоряет вычисления. Такой метод работает за время O(√n), что делает его гораздо быстрее при работе с большими числами.
В данной статье мы покажем, как реализовать этот подход на Python, используя встроенные функции и библиотеки для эффективного поиска делителей.
Как определить количество делителей для простого числа

Простое число имеет два делителя: 1 и само число. Это основная характеристика простого числа, отличающая его от составных чисел, которые имеют больше делителей. Чтобы определить количество делителей простого числа, достаточно понять, что их всегда два, независимо от величины числа.
Для проверки числа на простоту можно использовать алгоритм деления на все числа от 2 до квадратного корня из числа. Если число делится на любое из них без остатка, оно составное, иначе оно простое. Однако если число простое, то количество его делителей всегда равно двум.
В Python можно использовать этот факт для быстрого ответа на вопрос о количестве делителей простого числа. Не нужно вычислять все возможные делители, достаточно просто проверить его простоту. Если число простое, количество делителей всегда будет равно 2.
Пример кода для проверки простоты числа и подсчета количества его делителей:
def is_prime(n): if n <= 1: return False for i in range(2, int(n0.5) + 1): if n % i == 0: return False return True def count_divisors(n): return 2 if is_prime(n) else 0 # Простой случай для простого числа number = 29 print(count_divisors(number)) # Выведет 2, так как 29 – простое число
Этот код эффективно проверяет, является ли число простым, и если да, то возвращает количество его делителей – два.
Использование цикла для нахождения делителей числа

Пример на Python, который использует цикл для нахождения всех делителей числа:
def find_divisors(n):
divisors = []
for i in range(1, int(n0.5) + 1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n // i)
return divisors
Здесь цикл проходит от 1 до \( \sqrt{n} \), и для каждого делителя \( i \) добавляется пара \( i \) и \( n//i \), если \( i \) делит число \( n \). Это позволяет сократить количество итераций и ускорить работу программы.
Для чисел с большими значениями \( n \) такой подход значительно быстрее, чем проверка всех чисел до самого \( n \). Например, для числа 1000 цикл выполнит только 31 итерацию вместо 1000, что на 97% меньше.
Важно помнить, что если число является полным квадратом, то в процессе нахождения делителей для \( i = \sqrt{n} \) оба делителя будут одинаковыми, и они должны быть добавлены только один раз. В коде это контролируется условием: `if i != n // i`.
Как улучшить производительность поиска делителей с помощью квадратного корня

Для числа N делители всегда встречаются парами. Если A – делитель числа N, то существует делитель B, такой что A * B = N. Если A больше или равно √N, то B будет меньше или равен √N. Таким образом, достаточно проверять делители только до √N, что существенно уменьшает количество проверок.
Алгоритм оптимизации поиска делителей с использованием квадратного корня выглядит следующим образом:
- Вычислить √N и пройтись по всем числам от 1 до этого значения.
- Если число делит N, то добавлять оба делителя (A и B = N / A), если они не одинаковы.
Преимущества такого подхода:
- Число проверок делителей сокращается с N до √N.
- Для чисел порядка 10^6, при обычном методе поиска делителей потребуется порядка 10^6 итераций, в то время как с оптимизацией по квадратному корню – около 1000 итераций.
Пример кода для нахождения делителей числа с использованием квадратного корня:
import math def find_divisors(n): divisors = [] for i in range(1, int(math.sqrt(n)) + 1): if n % i == 0: divisors.append(i) if i != n // i: divisors.append(n // i) return divisors
Этот метод значительно повышает эффективность поиска делителей, особенно для больших чисел. Важно помнить, что проверка делителей до √N позволяет избежать лишних вычислений, минимизируя нагрузку на процессор и время выполнения программы.
Реализация алгоритма подсчёта делителей через факторизацию числа
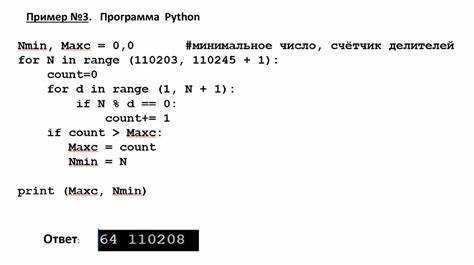
Для нахождения количества делителей числа через факторизацию необходимо разложить его на простые множители. Далее, используя их, можно вычислить количество делителей. Алгоритм факторизации чисел позволяет эффективно решать эту задачу, особенно для больших чисел.
Предположим, что мы хотим найти количество делителей числа N. Процесс можно разделить на несколько шагов:
- Разложение числа на простые множители: Для этого нужно попробовать делить число на все простые числа, начиная с 2. Если число делится на простое, продолжаем делить его, пока оно не перестанет делиться.
- Подсчёт степени каждого простого множителя: Для каждого простого множителя важно определить его степень. Степень простого множителя означает, сколько раз он входит в разложение числа.
- Вычисление количества делителей: Если число имеет разложение в виде:
N = p₁^e₁ * p₂^e₂ * … * pk^ek,
то количество делителей числа будет равно:
(e₁ + 1) * (e₂ + 1) * … * (ek + 1).
Рассмотрим пример:
- Число N = 60.
- Разлагаем 60 на простые множители: 60 = 2^2 * 3 * 5.
- Количество делителей числа 60: (2+1) * (1+1) * (1+1) = 3 * 2 * 2 = 12.
Алгоритм факторизации можно реализовать с использованием простого кода на Python. Пример реализации:
def count_divisors(n): divisors_count = 1 factor = 2 while factor * factor <= n: exponent = 0 while n % factor == 0: n //= factor exponent += 1 divisors_count *= (exponent + 1) factor += 1 if n > 1: divisors_count *= 2 return divisors_count
Этот код работает следующим образом:
- В начале инициализируется переменная divisors_count, которая будет хранить итоговое количество делителей.
- Алгоритм делит число на простые множители, начиная с 2. Для каждого простого множителя вычисляется его степень и увеличивает счётчик делителей.
- После завершения цикла проверки всех возможных делителей, если оставшееся число больше 1, это значит, что оно само является простым множителем.
Таким образом, факторизация позволяет быстро и эффективно находить количество делителей числа, особенно когда оно представлено как произведение небольших простых множителей. Этот метод лучше всего работает для чисел с небольшим количеством простых множителей, но остаётся эффективным и для более сложных случаев, если правильно использовать алгоритмы факторизации.
Как учесть кратные делители и избежать повторений
Для начала, когда ищется делитель числа, можно воспользоваться тем, что все делители числа встречаются по парам. Например, если число n делится на d, то d и n/d будут делителями. Таким образом, при проверке делителей до квадратного корня из числа, можно избежать повторов, так как если число n делится на d, то вторым делителем будет n/d.
Пример: для числа 36 делители будут 1, 2, 3, 4, 6, 9, 12, 18, 36. Но пары делителей (1, 36), (2, 18), (3, 12), (4, 9), (6, 6) встречаются несколько раз. Чтобы избежать повторений, можно сохранять только уникальные делители.
Также стоит учитывать, что делители числа могут быть кратными другим делителям. Например, число 36 имеет делители 2, 4, 6, 12, 18, которые являются кратными более мелким делителям (например, 4 – это кратное 2, а 6 – кратное 3). Для исключения кратных делителей следует проверять, что каждый делитель не был найден ранее и не является кратным другого уже добавленного делителя.
На практике это можно реализовать, используя множество, которое автоматически исключает повторяющиеся элементы. Например, при нахождении делителей числа можно добавлять их в множество, что гарантирует, что каждый делитель будет учтен только один раз, независимо от того, сколько раз он встречается в вычислениях.
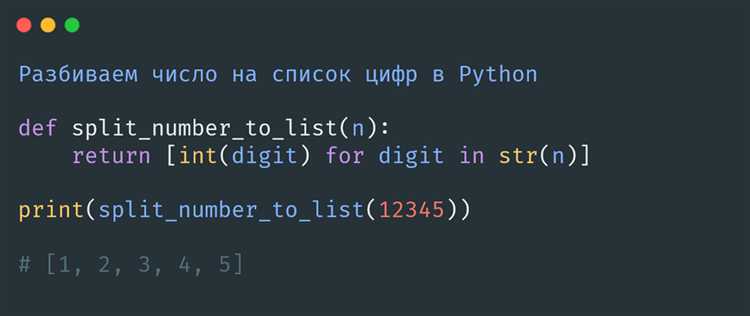
В Python для этого достаточно использовать конструкцию:
divisors = set() for i in range(1, int(n0.5) + 1): if n % i == 0: divisors.add(i) if i != n // i: divisors.add(n // i)
Этот код позволит получить только уникальные делители числа, при этом избегая повторений, даже если делители взаимно кратны друг другу.
Как проверить число на делимость перед поиском делителей
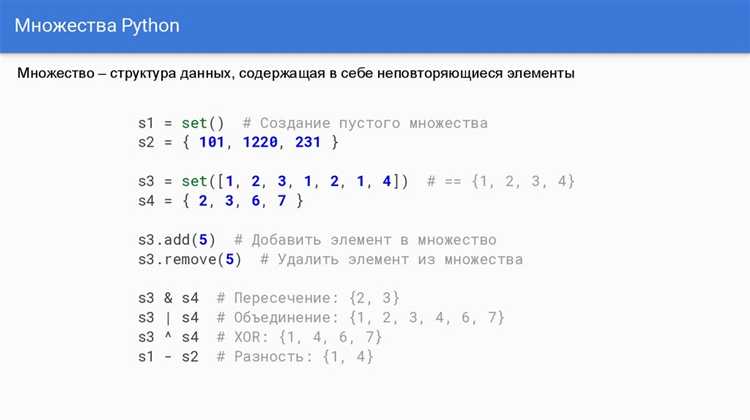
Перед перебором делителей полезно исключить заведомо неподходящие числа. Это снижает количество итераций и ускоряет выполнение кода. Простейшая проверка – делимость без остатка с помощью оператора %. Например, if n % 3 == 0 определяет, делится ли n на 3.
Для оптимизации следует начать с проверки на делимость наименьшими простыми числами: 2, 3, 5, 7. Если число не делится ни на одно из них, можно переходить к более крупным проверкам. Это особенно полезно при работе с большими числами.
Пример эффективной предварительной фильтрации:
def предварительная_проверка(n):
простые = [2, 3, 5, 7]
return any(n % p == 0 for p in простые)Если функция возвращает True, число делится хотя бы на одно из указанных простых чисел. Это позволяет либо сразу определить наличие делителей, либо начать дальнейший перебор с шагом, кратным найденному делителю.
Также полезно учитывать свойства четности: если n % 2 != 0, исключается половина всех возможных делителей. Аналогично, если n % 5 != 0, можно пропустить числа, оканчивающиеся на 0 или 5 при дальнейшем переборе.
Для сокращения количества проверок стоит ограничить перебор делителей корнем из числа:
for i in range(2, int(n 0.5) + 1):
if n % i == 0:
# найден делитель
Предварительная проверка на делимость – не просто фильтрация, а способ структурировать дальнейший алгоритм, исключив очевидные варианты.
Использование встроенных библиотек Python для поиска делителей
Модуль math предоставляет функцию isqrt(), которая позволяет эффективно ограничить диапазон перебора делителей квадратным корнем из числа. Это сокращает время выполнения алгоритма с O(n) до O(√n).
Пример с использованием math.isqrt():
import math
def count_divisors(n):
count = 0
for i in range(1, math.isqrt(n) + 1):
if n % i == 0:
count += 2 if i != n // i else 1
return count
Функция работает корректно для любых положительных целых чисел. Если число – полный квадрат, учтите, что делитель в корне учитывается один раз.
Для разложения числа на простые множители можно использовать collections.Counter совместно с ручной реализацией факторизации, чтобы затем подсчитать количество всех возможных делителей по формуле (e₁+1)(e₂+1)…(eₖ+1), где eᵢ – степень i-го простого множителя.
from collections import Counter
import math
def prime_factors(n):
i = 2
factors = []
while i * i <= n:
while n % i == 0:
factors.append(i)
n //= i
i += 1
if n > 1:
factors.append(n)
return Counter(factors)
def count_divisors_via_factors(n):
factors = prime_factors(n)
result = 1
for exp in factors.values():
result *= exp + 1
return result
Этот способ особенно полезен при необходимости многократного анализа различных чисел – можно кэшировать простые множители или использовать решето Эратосфена для ускорения факторизации.
Вопрос-ответ:
Что такое квадратный корень числа и почему его используют для нахождения делителей?
Квадратный корень числа — это число, которое при возведении в квадрат даёт исходное число. Например, квадратный корень из 36 — это 6, потому что \(6 \times 6 = 36\). Использование квадратного корня при нахождении делителей связано с тем, что делители числа идут парами, и одна из этих пар всегда будет меньше или равна квадратному корню. Например, для числа 36 делители: 1, 2, 3, 4, 6, 9, 12, 18, 36. Если мы нашли делитель 4, то знаем, что существует пара 36/4 = 9. Таким образом, достаточно проверить числа только до квадратного корня.






