Как найти обратную функцию mathcad

Обратная функция в Mathcad определяется как операция, позволяющая найти зависимость переменной исходя из известного результата функции. В отличие от ручных расчетов, Mathcad предлагает инструменты, которые значительно ускоряют этот процесс, минимизируя вероятность ошибок.

Для быстрого получения обратной функции используйте встроенную функцию root или оператор solve. Они позволяют задать уравнение исходной функции и получить значение переменной, а значит, эффективно найти обратную зависимость. Это особенно полезно при работе с функциями, не поддающимися простому аналитическому обращению.

Рекомендуется использовать численные методы решения уравнений в Mathcad при сложных функциях. Настройка начальных приближений в root повышает скорость сходимости. В случаях, когда требуется аналитическое выражение обратной функции, комбинируйте символические преобразования с численными вычислениями для проверки результатов.

Подготовка функции к вычислению обратной в Mathcad

Перед вычислением обратной функции в Mathcad важно задать функцию в явном виде с использованием операторов присваивания и правильно определить область её определения. Рекомендуется объявлять функцию через оператор :=, например, f(x):= выражение. Это обеспечит корректную интерпретацию Mathcad и упростит дальнейшую работу с функцией.

Для численного нахождения обратной функции необходимо ограничить область определения, чтобы исключить неоднозначности. Если функция многозначна, используйте условные операторы внутри определения, например, if или piecewise, чтобы зафиксировать нужный участок, на котором функция монотонна.

Важно проверить, что функция дифференцируема и не имеет точек разрыва на выбранном интервале, поскольку Mathcad использует численные методы, чувствительные к таким особенностям. При необходимости выполните предварительное построение графика, чтобы визуально оценить поведение функции.

Перед вычислением обратной функции задайте конкретный диапазон значений переменной, например, x ∈ [a, b], используя выражения типа range := a, a+step..b. Это позволит избежать ошибок при численном решении и сократит время вычислений.

В случае сложных функций рекомендуется вычислить производную f'(x) и убедиться, что её значения не равны нулю на выбранном интервале, что гарантирует существование обратной функции в пределах этой области.

Использование встроенных инструментов Mathcad для обратных функций

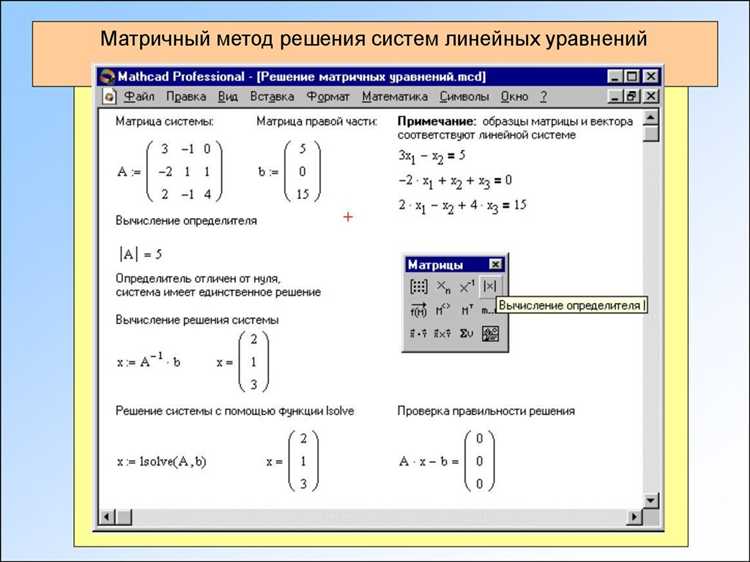
Mathcad предоставляет несколько эффективных способов получения обратной функции без ручного решения уравнений. Первый инструмент – оператор solve block, позволяющий задать уравнение вида y = f(x) и вычислить x через y. Для этого необходимо создать блок решения, в котором задать исходное уравнение и указать переменную для поиска.

Другой метод – функция Root, которая вычисляет корень уравнения. При определении обратной функции задается уравнение f(x) — y = 0, где y – известное значение, а x – переменная для нахождения. Важно указывать начальное приближение, чтобы ускорить сходимость и повысить точность результата.

Для функциональных выражений с явным аналитическим видом Mathcad позволяет использовать команду solve или Find для символического вычисления обратной функции, если это возможно. При этом система автоматически упрощает выражение, что экономит время по сравнению с ручным преобразованием.

Также полезно применять встроенный графический анализ – построить графики исходной и предполагаемой обратной функции, чтобы визуально проверить корректность решения. Mathcad поддерживает динамические переменные, что облегчает настройку и отладку вычислений.

Использование встроенных средств Mathcad значительно ускоряет процесс нахождения обратной функции и минимизирует ошибки, особенно при работе с комплексными выражениями и численными методами.

Метод численного поиска обратной функции в Mathcad

Для поиска обратной функции в Mathcad без аналитического выражения используется численный метод, основанный на решении уравнения исходной функции относительно переменной. Главное – задать функцию как оператор, например, f(x):= выражение, и определить область значений.

Для вычисления обратного значения при заданном аргументе y применяется встроенная функция root(). Синтаксис: root(f(x)-y, x, x0), где y – значение функции, x – переменная, по которой ищется корень, x0 – начальное приближение.

Выбор начального приближения критичен для сходимости. Рекомендуется использовать приближенное значение из области определения функции, где f(x) близка к y. Если область невелика, можно задать несколько точек для повышения точности.

Для построения обратной функции создайте вектор значений y с нужным шагом, затем примените к каждому элементу вектора оператор root(), получая соответствующие значения x. Такой подход позволяет быстро получить массив значений обратной функции.

Важный момент – функция должна быть монотонной на рассматриваемом интервале. При наличии нескольких корней необходимо вручную ограничить область поиска через параметры root() или разбить задачу на подынтервалы.

Использование метода root() эффективно при сложных выражениях, где аналитическое решение затруднено или невозможно. Он обеспечивает достаточную точность, ограниченную параметрами итерации и выбором начального приближения.

Автоматизация нахождения обратной функции с помощью скриптов

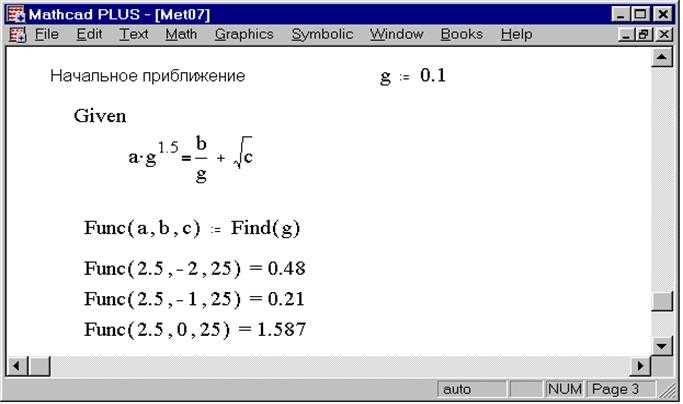
Для быстрого получения обратной функции в Mathcad целесообразно применять встроенный скриптовый язык Prime или языки автоматизации, поддерживаемые внешними надстройками, например Python с библиотекой Mathcad-Python API. Основной принцип – задать уравнение исходной функции и автоматически решить его относительно переменной аргумента.

Пример на Mathcad Prime: создайте скрипт, который принимает исходную функцию f(x) и использует оператор solve для поиска y, где f(y) = x. Такой подход позволяет быстро получать аналитическое выражение обратной функции при условии ее существования.

Для сложных функций, где аналитическое решение затруднено, рекомендуются численные методы – реализовать итерационный алгоритм обратной подстановки с контролем сходимости. В Mathcad это можно сделать с помощью циклов и функций поиска корня, например, root или find.

Для интеграции в рабочие процессы полезно оформлять скрипты в виде функций с параметрами, позволяющими менять исходную функцию и диапазон поиска без переписывания кода. Это значительно ускоряет обработку множества задач с различными исходными данными.

Рекомендации:

• Используйте Mathcad Prime с поддержкой программирования на встроенном языке для максимальной совместимости.
• Автоматизируйте проверку существования обратной функции через анализ монотонности или производной.
• При численных методах задавайте начальные приближения на основе графического анализа.
• Внедряйте обработку ошибок и условия остановки в циклах, чтобы избежать бесконечных вычислений.

Проверка правильности обратной функции в Mathcad

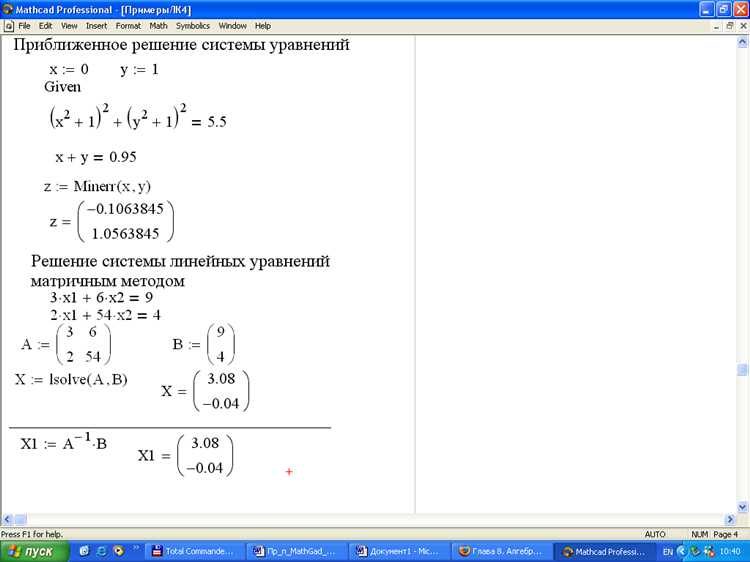
После построения обратной функции в Mathcad необходимо убедиться в её корректности. Для этого достаточно подставить исходные значения в композицию функций: f(f⁻¹(x)) и f⁻¹(f(x)). Результатом обеих операций должна быть функция тождественного отображения, то есть значение аргумента x.

В Mathcad создайте две новых переменных, например, check1 := f(f_inv(x)) и check2 := f_inv(f(x)), где f_inv – обратная функция. Постройте графики check1 и check2 на интервале, соответствующем области определения исходной и обратной функций. Если графики совпадают с прямой y = x, обратная функция определена верно.

Дополнительно можно проверить численные значения в ключевых точках, например, в точках разрыва или экстремума исходной функции. Введите конкретные значения аргумента и сравните результат вычисления f(f_inv(x)) и f_inv(f(x)) с самим x. Отклонение не должно превышать машинной точности Mathcad.

Используйте встроенную функцию abs для вычисления ошибки: error := abs(check1 — x). Если максимальное значение error на выбранном интервале не превышает 10⁻¹², результат считается точным.

При работе с параметрическими функциями или функциями с несколькими переменными проверка сводится к аналогичной процедуре с фиксированными параметрами, учитывая область определения и значения параметров.

Частые ошибки при вычислении обратной функции и как их избежать

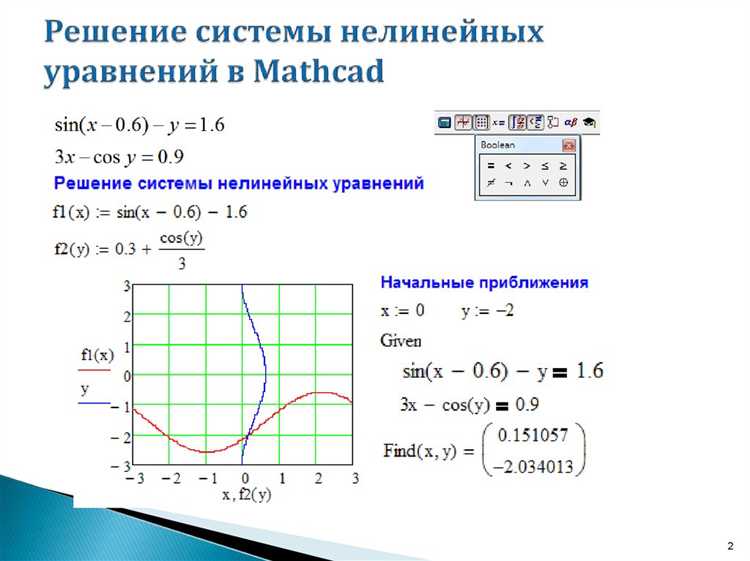
В Mathcad при поиске обратной функции часто возникают ошибки, которые связаны с неправильным подходом или упущением ключевых моментов. Чтобы работать эффективно, нужно учитывать следующие нюансы:

• Игнорирование области определения функции. Обратная функция существует только при однозначном соответствии значений. Если функция не монотонна или не ограничена, Mathcad может построить неверную обратную. Перед вычислением проверьте, что функция строго возрастает или убывает на рассматриваемом промежутке.
• Использование численных методов без начального приближения. При вычислении обратной функции через численное решение уравнения f(x) = y важно задавать начальное приближение для переменной x. Без этого Mathcad может не сойтись к решению или выдаст неверный результат.
• Отсутствие указания переменной для обратной функции. В Mathcad необходимо явно определить переменную, по которой строится обратная функция. Без этого инструмент не сможет корректно интерпретировать выражение и построить обратную.
• Попытка обращения функции с несколькими значениями на одно входное. Например, обратная функция от y = x² не существует без ограничения области. В Mathcad следует использовать дополнительные условия, чтобы сузить область и получить однозначное соответствие.
• Пренебрежение проверкой результата. После вычисления обратной функции обязательно подставляйте значения из области определения, чтобы проверить, что f⁻¹(f(x)) = x. Если равенство не выполняется, значит, допущена ошибка в вычислениях или в постановке задачи.

Чтобы избежать ошибок, рекомендуется:

1. Перед построением обратной функции проанализировать поведение исходной функции, особенно на предмет монотонности.
2. Использовать встроенные инструменты Mathcad для задания ограничений и начальных приближений при численных вычислениях.
3. Всегда проверять корректность обратной функции подстановкой и визуальным сравнением графиков исходной и обратной функций.
4. Использовать именованные переменные и четко структурировать выражения для повышения читаемости и уменьшения риска ошибок.

Вопрос-ответ:

Как в Mathcad быстро определить, существует ли обратная функция для заданной?

В Mathcad можно проверить обратимость функции, анализируя её поведение: если функция монотонна на рассматриваемом промежутке, то обратная функция существует. Для численного подтверждения можно построить график функции и убедиться, что она проходит тест на горизонтальную прямую — любая горизонтальная линия пересекает график не более одного раза.

Какие инструменты Mathcad помогают найти обратную функцию без ручных вычислений?

В Mathcad удобно использовать встроенную команду для численного решения уравнений, такую как solve или root, чтобы выразить переменную исходя из значения функции. Это позволяет получить значения обратной функции без необходимости вручную решать уравнение, особенно если аналитическое выражение сложно.

Можно ли в Mathcad получить формулу обратной функции в символическом виде?

Да, Mathcad поддерживает символические вычисления, и если функция задана выражением, допускающим обратное преобразование, можно применить команду для решения уравнения относительно исходной переменной. Однако для сложных функций этот процесс может не привести к простому выражению, тогда лучше использовать численные методы.

Как быстро проверить корректность найденной обратной функции в Mathcad?

Чтобы убедиться, что найденная функция является обратной, достаточно подставить её в исходную функцию и убедиться, что результат близок к аргументу. В Mathcad можно вычислить композицию функции и её обратной для нескольких значений и проверить совпадение с исходными значениями.

Что делать, если обратная функция не выражается явно в Mathcad?

В случаях, когда найти аналитическую форму обратной функции невозможно, в Mathcad можно использовать численные методы: задать уравнение f(x) = y и решить его для x при различных y с помощью встроенных функций поиска корня. Таким образом, строится численное представление обратной функции, позволяющее получить приближённые значения.

Как в Mathcad быстро найти обратную функцию для заданного выражения?

В Mathcad для нахождения обратной функции обычно используют численные методы или инструменты решения уравнений. Например, можно задать исходную функцию, а затем применить команду решения уравнения относительно переменной, которая является аргументом функции, чтобы получить обратную зависимость. Такой подход особенно удобен для функций, которые нельзя легко обратить аналитически.