Wolfram Mathematica предоставляет эффективные инструменты для вычисления собственных векторов и собственных значений матриц любой размерности. Встроенная функция Eigenvectors позволяет быстро получить набор собственных векторов, упорядоченных в соответствии с собственными значениями.
Для точного анализа стоит учитывать тип матрицы: симметричные, эрмитовы или общие матрицы могут требовать различных подходов к интерпретации результатов. Например, для вещественных симметричных матриц собственные векторы всегда ортогональны, что удобно для последующих вычислений и упрощает проверку корректности.
Рекомендуется предварительно проверить матрицу на вырожденность с помощью функции Det, поскольку наличие нулевого определителя может означать кратные собственные значения, что влияет на число и структуру собственных векторов. В Mathematica также можно получить собственные значения и векторы одновременно через функцию EigenSystem, что оптимизирует вычисления и упрощает обработку результатов.
Как задать матрицу для поиска собственных векторов в Mathematica

В Mathematica матрица задаётся как список списков чисел, где каждый внутренний список представляет строку матрицы. Например, квадратную матрицу 3×3 можно определить так:
A = {{a11, a12, a13}, {a21, a22, a23}, {a31, a32, a33}};
Элементы aij могут быть целыми, рациональными или действительными числами. Для точных вычислений предпочтительно использовать дроби в формате n/d вместо десятичных дробей.
Важно, чтобы все строки содержали одинаковое количество элементов, иначе Mathematica выдаст ошибку при обработке матрицы.
Для создания больших матриц удобно применять функции Table или Array. Например:
A = Table[If[i == j, 2, 1], {i, 3}, {j, 3}];
создаст матрицу с 2 на диагонали и 1 в остальных позициях.
Перед поиском собственных векторов убедитесь, что матрица корректно определена и не содержит символических неопределённых элементов, если требуется численное решение.
Использование функции Eigenvectors для вычисления собственных векторов

В Wolfram Mathematica функция Eigenvectors вычисляет собственные векторы квадратной матрицы. Она возвращает список векторов, каждый из которых соответствует собственному значению матрицы в порядке убывания.
- Входной параметр – матрица типа
n×n. Матрица должна быть числовой или символьной с числовыми значениями. - Для вычисления собственных векторов матрицы
Aдостаточно вызватьEigenvectors[A]. Результат – список изnвекторов-столбцов. - Векторы нормализованы по умолчанию, то есть имеют длину 1. Для получения ненормализованных векторов используйте опцию
Method -> "Raw". - Если необходимо вычислить только первые
kсобственных векторов, укажите второй аргумент:Eigenvectors[A, k]. Это ускоряет вычисления при больших матрицах. - Функция корректно работает с матрицами комплексных чисел, возвращая комплексные собственные векторы.
Пример использования:
A = {{4, 1}, {2, 3}};
ev = Eigenvectors[A]
Результат содержит два собственных вектора, соответствующих собственным значениям матрицы A.
Для проверки корректности вычислений рекомендуется использовать функцию Eigensystem, которая возвращает одновременно и собственные значения, и собственные векторы:
{values, vectors} = Eigensystem[A];
Собственные векторы из Eigenvectors и vectors совпадают по направлениям и нормировке.
Функция Eigenvectors оптимизирована для численных расчетов и находит все собственные векторы без дополнительной настройки. В случае символьных матриц вычисления могут быть более ресурсоемкими, поэтому рекомендуется предварительно упростить матрицу.
Обработка комплексных собственных векторов и их интерпретация
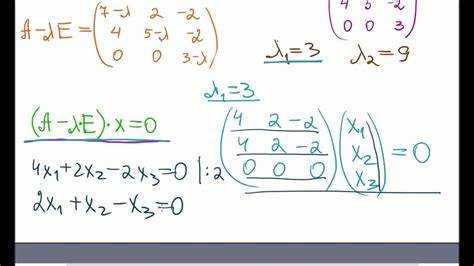
- Получение комплексных собственных векторов: функция
Eigenvectors[matrix]возвращает векторы с комплексными компонентами при наличии комплексных собственных значений. Для точного вычисления рекомендуется использовать высокоточные типы данных, например,SetPrecision. - Нормализация: комплексные собственные векторы нормируют по комплексной норме, используя
Norm[vector], которая вычисляет квадратный корень суммы квадратов модулей компонент. Важна единообразная нормировка для последующего сравнения и визуализации. - Фазовая неопределённость: собственный вектор определён с точностью до умножения на комплексное число с модулем 1. Для устранения неоднозначности обычно нормируют так, чтобы первая ненулевая компонента имела положительную действительную часть или нулевую мнимую часть.
- Визуализация: для комплексных собственных векторов удобны графики амплитуд и аргументов компонент. В Mathematica подходят функции
ListPlotиComplexExpandдля разложения на вещественную и мнимую части, а такжеArgдля вычисления фаз. - Интерпретация в приложениях:
- В динамических системах комплексные собственные векторы связаны с колебательными режимами, где мнимая часть собственных значений задаёт частоту колебаний.
- В квантовой механике такие векторы описывают состояния с комплексной амплитудой вероятности, важны фаза и модуляция сигнала.
Для анализа комплексных собственных векторов рекомендуется проводить дополнительное сравнение с сопряжёнными векторами, а при необходимости использовать функцию Chop для удаления численных шумов порядка машинного эпсилон.
При решении практических задач можно выделить компоненты векторов с большими модулями для упрощения модели и более наглядной интерпретации результатов.
Настройка точности и числовые особенности вычислений

При поиске собственных векторов в Wolfram Mathematica важно учитывать формат и точность числовых данных. По умолчанию функции работают с машинной точностью (~16 знаков), что может приводить к накоплению погрешностей на этапах решения характеристического уравнения и последующей нормализации векторов.
Для повышения точности используйте функцию SetPrecision, задавая необходимое количество значащих цифр до начала вычислений, например: SetPrecision[matrix, 50]. Это особенно актуально для матриц с близкими или почти кратными собственными значениями, где малейшая ошибка может изменить спектр.
Функция Eigenvectors автоматически адаптирует внутренние алгоритмы к точности входных данных. Если исходные данные – числа с плавающей точкой низкой точности, результат будет ограничен этой точностью. Для контролируемого повышения точности применяйте вычисления в режиме произвольной точности с WorkingPrecision, например: Eigenvectors[matrix, WorkingPrecision -> 50].
При использовании произвольной точности стоит учитывать увеличение времени вычислений и памяти. Оптимальным балансом является выбор точности в пределах 30-50 знаков, что значительно снижает ошибки без чрезмерных затрат ресурсов.
Числовые особенности включают также вопросы устойчивости при вычислении собственных векторов для плохо обусловленных матриц. Для таких случаев рекомендуют использовать предварительную нормализацию матрицы или функции типа Chop для отсечения малых погрешностей после вычислений.
При анализе комплексных собственных значений и векторов важно использовать точность, обеспечивающую корректное определение знаков и фаз. Низкая точность приводит к искажению аргументов комплексных чисел и неверной интерпретации геометрии собственных пространств.
Резюмируя, контроль точности через SetPrecision и WorkingPrecision – ключевой инструмент при вычислении собственных векторов в Mathematica, особенно для задач с высокой чувствительностью к ошибкам округления и при работе с большими или плохо обусловленными матрицами.
Визуализация собственных векторов с помощью встроенных средств Mathematica
Для визуализации собственных векторов матрицы в Mathematica оптимально применять функцию Eigenvectors совместно с графическими средствами. Сначала вычисляют собственные векторы, например, v = Eigenvectors[matrix]. При работе с двумерными и трёхмерными матрицами целесообразно использовать Graphics и Graphics3D соответственно.
Для 2D-векторов удобно отображать их как стрелки с помощью Arrow. Например, команда Graphics[{Arrow[{{0, 0}, #}]} & /@ v] отобразит все собственные векторы, исходящие из начала координат. Можно добавить оси и сетку через Axes -> True и GridLines -> Automatic для удобства восприятия.
При работе с 3D-векторами применяется Graphics3D с объектами Arrow, например, Graphics3D[{Arrow[{{0, 0, 0}, #}] & /@ v}]. Для масштабирования векторов рекомендуется нормировать их длину или задавать параметр ScalingFunctions. Это предотвращает визуальное перекрытие при больших значениях компонент.
Для наглядности можно использовать цветовую дифференциацию собственных векторов, применяя списки цветов: Graphics[{Red, Arrow[...]}, {Blue, Arrow[...]}]. Автоматическую генерацию палитры обеспечивает функция ColorData["Rainbow"] с параметризацией по индексу вектора.
Для комплексных собственных векторов можно использовать проекции на действительную и мнимую части, визуализируя их в 2D или 3D пространстве как отдельные объекты. Пример: Re[v] и Im[v] отображаются разными цветами или стилями линий.
Использование встроенных средств Mathematica позволяет создавать интерактивные визуализации через Manipulate, варьируя параметры матрицы и мгновенно наблюдая изменение собственных векторов в пространстве.
Применение собственных векторов в решении прикладных задач в Mathematica

Собственные векторы матриц в Mathematica широко используются для анализа систем в механике, экономике и обработке данных. В механике, например, нахождение собственных векторов матрицы жесткости позволяет определить направления нормальных колебаний конструкции. Для этого в Mathematica применяется команда Eigenvectors[matrix], возвращающая векторы, на которых действует система без изменения направления.
В финансовом моделировании собственные векторы ковариационных матриц активов помогают выделить основные факторы риска. Использование Eigenvectors совместно с Eigenvalues позволяет построить факторные модели и оптимизировать портфель. Рекомендуется нормировать собственные векторы для сравнимости вкладов факторов.
В машинном обучении собственные векторы используются для уменьшения размерности данных с помощью метода главных компонент (PCA). В Mathematica можно вычислить их через Eigensystem[dataCovarianceMatrix]. При этом собственные векторы с наибольшими собственными значениями выбираются для проекции данных, что снижает шум и ускоряет обучение моделей.
Для практического применения важно учитывать точность вычислений: в Mathematica можно контролировать её с помощью функций SetPrecision и WorkingPrecision при вычислении собственных векторов. Это особенно актуально при работе с матрицами большого размера или близкими по значению собственными числами.
Пример вычисления и нормировки собственных векторов в Mathematica:
mat = {{4, 1}, {1, 3}};
{vals, vecs} = Eigensystem[mat];
normVecs = Normalize /@ vecs;
normVecs
В итоге нормированные собственные векторы можно напрямую использовать для анализа направлений влияния в моделируемой системе, что повышает информативность прикладных решений.
Вопрос-ответ:
Как в Wolfram Mathematica найти собственные значения и собственные векторы заданной матрицы?
Для поиска собственных значений и собственных векторов в Mathematica используется функция Eigenvectors для векторов и Eigenvalues для значений. Если нужно получить их вместе, можно применить функцию Eigensystem, которая возвращает список пар — собственный вектор и соответствующее собственное значение. Например, для матрицы A вызов Eigensystem[A] выдаст все собственные векторы и собственные значения.
Какие особенности стоит учитывать при вычислении собственных векторов для матриц с комплексными элементами в Mathematica?
Wolfram Mathematica корректно работает с матрицами, содержащими комплексные числа. При вычислении собственных векторов для таких матриц функция Eigenvectors возвращает векторы с комплексными компонентами. Следует помнить, что собственные векторы определены с точностью до умножения на ненулевой скаляр, и результат может содержать комплексные константы, что естественно при работе с комплексными матрицами.
Можно ли задать пользовательские параметры или ограничить вычисления при поиске собственных векторов в Mathematica?
Да, Mathematica предоставляет возможность уточнять вычисления. Например, в функции Eigenvalues можно указать количество искомых собственных значений, а также метод вычисления с помощью опций. Для больших разреженных матриц применяется функция SparseArray вместе с методами, оптимизированными для таких случаев. Это позволяет снизить вычислительную нагрузку и ускорить процесс.
Как интерпретировать результат функции Eigensystem при работе с вырожденными матрицами?
Вырожденные матрицы имеют повторяющиеся собственные значения, и в таких случаях соответствующие собственные векторы могут не быть уникальными. Mathematica выдаст базис собственных векторов для каждого собственного значения с кратностью больше единицы. Это значит, что функция Eigensystem вернёт несколько векторов, которые образуют пространство собственных векторов, связанное с данным собственным значением.
Как использовать найденные собственные векторы для дальнейшего анализа или преобразований в Mathematica?
Собственные векторы часто применяются для диагонализации матриц, анализа устойчивости систем или упрощения выражений. В Mathematica можно построить матрицу из собственных векторов, а затем с её помощью преобразовать исходную матрицу к диагональному виду через операцию similarity transform. Это позволяет работать с матрицей в более удобном формате, например, для вычисления степеней или функций от матрицы.
Какие функции Wolfram Mathematica можно использовать для нахождения собственных векторов матрицы?
В Wolfram Mathematica для поиска собственных векторов матриц чаще всего применяется функция Eigenvectors. Она принимает на вход матрицу и возвращает список векторов, соответствующих собственным значениям этой матрицы. Кроме того, можно использовать функцию Eigensystem, которая возвращает одновременно и собственные значения, и собственные векторы. Для численных и аналитических вычислений доступен широкий набор опций, позволяющих управлять точностью и форматом результата.
Как работать с комплексными собственными векторами в Mathematica и можно ли визуализировать их?
При работе с матрицами, у которых собственные векторы имеют комплексные компоненты, Mathematica обрабатывает их без проблем, возвращая комплексные числа в виде a + b I. Для визуализации таких векторов можно использовать функции графики, например, VectorPlot или ListVectorPlot, но в этом случае требуется разбить комплексные векторы на действительную и мнимую части или использовать их модуль и аргумент. Это помогает лучше понять структуру и направление векторов в комплексном пространстве. Также возможно строить 3D-графики с помощью Graphics3D, если дополнительно определять представление комплексных чисел в трехмерной форме.