Как найти спектр сигнала в mathcad

Для анализа спектра сигнала в Mathcad важно точно определить тип сигнала и задать корректные параметры преобразования Фурье. Mathcad позволяет использовать встроенные функции для вычисления спектральных характеристик, но результат напрямую зависит от правильной подготовки данных и настройки дискретизации.

Первый шаг – сформировать в Mathcad массив исходных данных сигнала с равномерным шагом по времени. Этот шаг определяет максимальную частоту, которую можно корректно проанализировать (частота Найквиста). Затем необходимо применить дискретное преобразование Фурье с использованием функции fft или собственноручно реализованного алгоритма для повышения точности.

Далее важно правильно интерпретировать полученный спектр: масштабировать амплитуды с учётом длины выборки и выделить полезные гармоники. Рекомендуется визуализировать спектр с помощью графиков Mathcad, используя подписи и легенды для удобства анализа. Такая последовательность действий позволяет получить детальный спектральный разбор и выявить частотные составляющие сигнала с минимальными искажениями.

Подготовка исходных данных для анализа сигнала в Mathcad

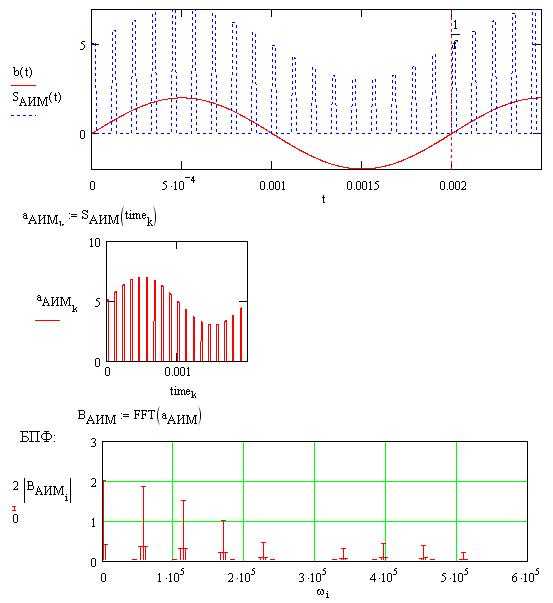
Для корректного поиска спектра сигнала в Mathcad требуется точная и структурированная подготовка исходных данных. Необходимо обеспечить однородность и точность временной базы и амплитудных значений.

1. Определите дискретизацию сигнала:
   • Задайте постоянный шаг дискретизации Δt, чтобы временные точки были равномерно распределены.
   • Обеспечьте частоту дискретизации, как минимум вдвое превышающую максимальную частоту сигнала (теорема Найквиста).
2. Задайте временной интервал:
   • Выберите начало и конец временного окна, в котором представлен сигнал.
   • Количество точек должно быть степенью двойки для оптимизации вычисления БПФ (быстрого преобразования Фурье).
3. Подготовьте вектор времени:
   • Используйте оператор диапазона или функцию генерации последовательности для создания массива времени.
   • Проверьте правильность размерности и последовательности элементов.
4. Внесите амплитудные значения сигнала:
   • Импортируйте данные из внешнего источника или задайте аналитическую формулу.
   • Проверьте отсутствие пропусков и шумов, влияющих на спектральный анализ.
5. Обеспечьте единообразие единиц измерения:
• Время – в секундах, амплитуда – в вольтах или других стандартизованных единицах.
• Единицы должны соответствовать задачам дальнейшего анализа.
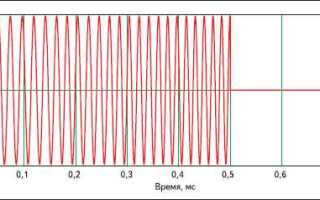
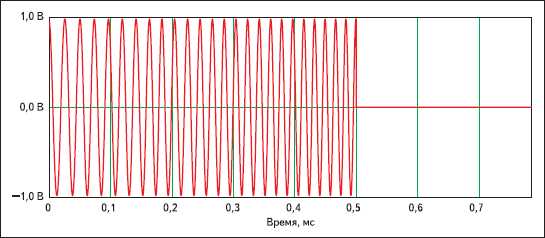
6. Произведите визуальную проверку исходного сигнала в Mathcad:
   • Постройте график временной зависимости для выявления аномалий.
   • Убедитесь в корректности масштабов и отсутствия выбросов.

Строгая подготовка исходных данных обеспечит надежность и точность спектрального анализа в Mathcad, минимизируя ошибки, связанные с неправильной дискретизацией и структурированием сигнала.

Настройка временного интервала и дискретизации сигнала

Для точного анализа спектра в Mathcad важно корректно определить временной интервал и шаг дискретизации. Эти параметры напрямую влияют на разрешение частотного спектра и качество преобразования Фурье.

1. Выбор временного интервала (T)

   • Интервал должен покрывать минимум один полный период исследуемого сигнала или его значимую часть.
   • Оптимально выбирать T как кратное периоду сигнала, чтобы избежать искажений спектра.
   • Слишком короткий интервал снижает частотное разрешение (Δf = 1/T), увеличивая ширину спектральных линий.

2. Определение шага дискретизации (Δt)

   • Шаг должен удовлетворять условию Найквиста: Δt ≤ 1/(2f_max), где f_max – максимальная частота сигнала.
   • Меньший Δt обеспечивает большее количество отсчетов и улучшает точность, но увеличивает вычислительную нагрузку.
   • В Mathcad рекомендуется задать Δt так, чтобы число отсчетов N = T/Δt было степенью двойки для оптимизации алгоритма FFT.

3. Практические рекомендации в Mathcad

   • Задайте вектор времени с равномерным шагом: t := 0, Δt .. T - Δt.
   • Проверьте, что количество точек N совпадает с размером сигнала и соответствует степеням двойки.
   • Для анализа несинусоидальных сигналов увеличьте T, чтобы получить более детализированный спектр.

Вычисление преобразования Фурье для сигнала в Mathcad

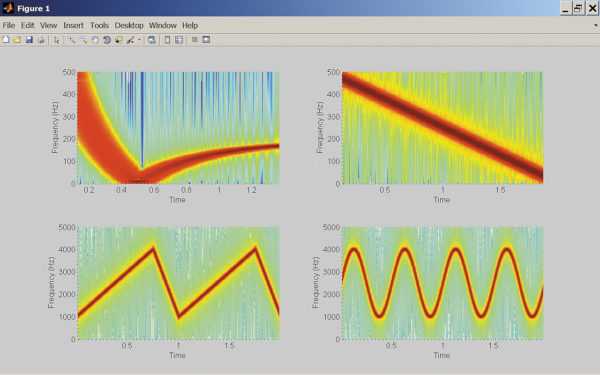
Для точного вычисления преобразования Фурье в Mathcad используйте встроенную функцию FFT, которая реализует быстрый алгоритм преобразования Фурье. Начните с задания временного массива с равномерным шагом, например, t := 0, Δt .. T, где Δt – интервал дискретизации, а T – конечное время наблюдения. Затем определите сигнал как функцию от времени: f(t).

Перед применением FFT убедитесь, что длина массива сигнала является степенью двойки, иначе результат будет некорректен или потребует дополнительной интерполяции. Если длина не соответствует, дополните сигнал нулями или обрежьте до ближайшего значения 2^n.

Вызов функции преобразования выглядит так: F := fft(f). Mathcad вернет комплексный массив, представляющий амплитуды и фазы спектральных компонент. Для получения модуля спектра используйте |F|, а для вычисления частотного вектора применяйте формулу freq := k / (N * Δt), где k = 0..N-1, а N – длина сигнала.

Для правильной интерпретации спектра важно учитывать, что результирующий вектор частот содержит как положительные, так и отрицательные частоты. При анализе реальных сигналов рассматривайте только половину спектра до Nyquist frequency = 1/(2Δt).

Результат можно визуализировать, построив график зависимости модуля спектра от частоты. Для улучшения точности и уменьшения утечек спектра рекомендуется предварительно применять оконные функции, такие как Хэмминга или Ханна, перед вычислением FFT.

Построение графика амплитудного спектра сигнала

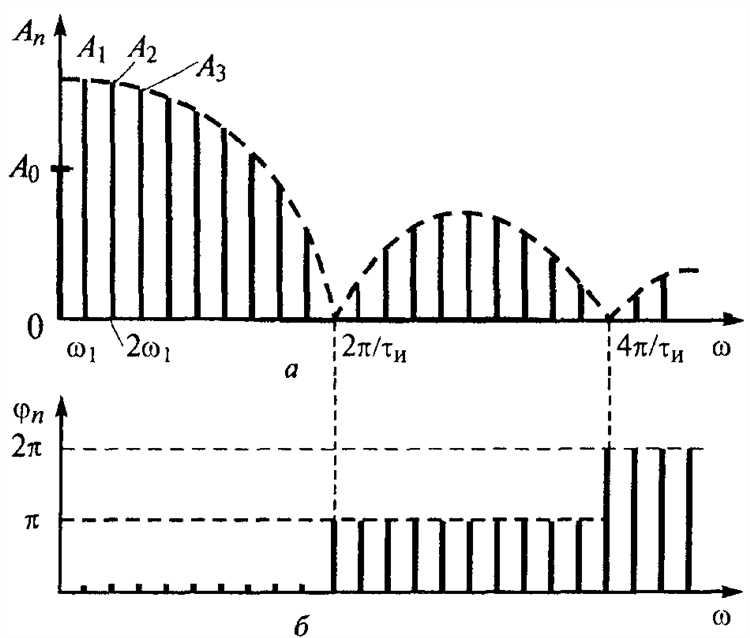
Для построения амплитудного спектра в Mathcad сначала выполните дискретное преобразование Фурье (ДПФ) исходного сигнала. Используйте функцию fft, задав массив значений сигнала и количество точек преобразования, обычно равное длине сигнала или ближайшей степени двойки для оптимизации.

После вычисления комплексного спектра получите амплитудный спектр, вычислив модуль каждого комплексного значения: амплитуда = abs(fft_результат). Для нормализации разделите полученные амплитуды на количество отсчетов, чтобы масштаб соответствовал исходному сигналу.

Для отображения спектра создайте вектор частот. Он формируется по формуле f = (0:N-1) * (Fs/N), где N – количество точек ДПФ, а Fs – частота дискретизации.

При построении графика выберите диапазон частот до половины частоты дискретизации (до Fs/2), так как выше этого значения спектр симметричен и не содержит новой информации.

В Mathcad используйте встроенный инструмент графиков: задайте ось X – частоты, ось Y – амплитуды. Убедитесь, что масштаб осей позволяет четко видеть пики спектра. При необходимости примените логарифмическую шкалу по оси Y для улучшения визуализации малых амплитуд.

Определение частотных компонент сигнала по спектру

Для выявления частотных компонентов сигнала в Mathcad сначала необходимо выполнить преобразование Фурье. Используйте встроенную функцию FFT, задав массив исходных значений сигнала и шаг дискретизации по времени. Результатом будет комплексный массив спектра.

Амплитуды частотных компонентов получают как модуль комплексных значений спектра: вычислите √(Re² + Im²) для каждого элемента. Для отображения значимых частот следует нормировать амплитуды на длину сигнала и выделить пики, превосходящие заданный порог, например 10% от максимальной амплитуды.

Частоты соответствуют индексам элементов спектра, умноженным на частоту дискретизации и делённым на количество точек. Формула: f = i * Fs / N, где i – индекс, Fs – частота дискретизации, N – число точек.

Для точного определения частотных компонентов рекомендуется использовать нулевое дополнение (zero-padding) перед FFT. Это увеличит разрешение по частоте, позволяя точнее локализовать пики спектра.

Если спектр содержит шум, примените фильтрацию: например, сглаживание методом скользящего среднего по амплитуде спектра или пороговую фильтрацию по уровню амплитуды. Это упростит выделение основных частот.

Итоговая частотная составляющая сигнала – это набор частот и соответствующих им амплитуд, выявленных как локальные максимумы спектра после нормализации и фильтрации. Полученные значения можно использовать для дальнейшего анализа или синтеза сигнала.

Использование фильтрации для выделения нужных частот в Mathcad

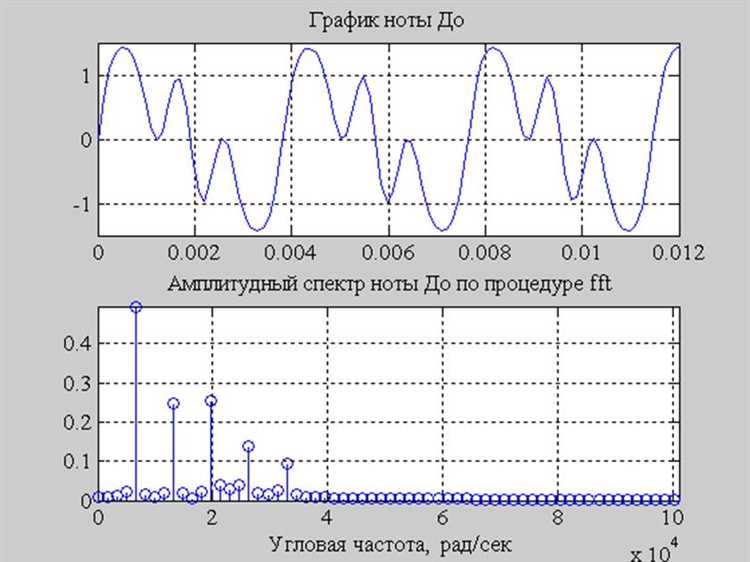
В Mathcad фильтрация сигналов реализуется с помощью функций обработки массивов данных и встроенных функций цифровой фильтрации. Для выделения частотного диапазона сначала необходимо получить дискретный сигнал и его спектр, например, через преобразование Фурье с помощью функции fft.

Далее фильтр создаётся как вектор коэффициентов, соответствующих пропусканию или подавлению определённых частот. Для полосового фильтра создайте логический массив, в котором частоты внутри диапазона установлены в 1, вне диапазона – в 0. Этот массив умножается на спектр сигнала, что исключает нежелательные частоты.

При реализации фильтра обратите внимание на разрешающую способность спектра, зависящую от длины выборки и частоты дискретизации. Чем выше разрешение, тем точнее можно выделить узкие полосы частот.

Для сглаживания переходов между пропускаемыми и подавляемыми частотами применяйте оконные функции (например, Ханна или Хэмминга), уменьшающие эффекты утечки спектра. В Mathcad окно формируется отдельным массивом и умножается на исходный сигнал перед преобразованием Фурье.

В качестве альтернативы можно использовать цифровые фильтры с конечной импульсной характеристикой (FIR), проектируемые через последовательность коэффициентов. Для этого вручную задайте коэффициенты, или используйте внешние утилиты, результаты которых импортируйте в Mathcad для свёртки с сигналом.

После фильтрации восстановите сигнал из изменённого спектра обратным преобразованием Фурье (ifft). Проверьте качество фильтрации, сравнив спектры исходного и обработанного сигналов, а также визуализируя временные области.

Сравнение спектров разных сигналов с помощью Mathcad

Для сравнения спектров нескольких сигналов в Mathcad необходимо построить их частотные характеристики на одном графике. Это позволяет выявить различия в амплитудном и частотном содержании сигналов, определить доминирующие гармоники и уровень шумов.

Шаг 1. Определите временные функции сигналов, например, f1(t) и f2(t). Убедитесь, что временные интервалы и шаг дискретизации совпадают для обоих сигналов, иначе спектры будут несопоставимы.

Шаг 2. Выполните дискретное преобразование Фурье (ДПФ) для каждого сигнала с помощью встроенной функции Mathcad fft(). Результаты обозначьте как F1(f) и F2(f). Для удобства масштабируйте амплитуду спектров, разделив на количество точек выборки.

Шаг 3. Постройте графики амплитудных спектров на одной координатной плоскости с одинаковым диапазоном частот. Используйте ось X в герцах, а ось Y – в относительных единицах амплитуды.

Рекомендуется выделить разные сигналы цветом или типом линий для наглядности. Например, первый сигнал – сплошной синий, второй – пунктирный красный.

Шаг 4. Анализируйте спектры с учетом ключевых параметров:

• Положение пиков по частоте укажет на основные гармоники.
• Ширина пиков отражает устойчивость и длительность периодов сигнала.
• Уровень шумового фона помогает оценить качество сигнала.

Для точного сравнения рекомендуется использовать нормализацию спектров к максимальному значению амплитуды каждого сигнала. Mathcad позволяет добавить к графику легенду с наименованиями сигналов, что упрощает интерпретацию результатов.

При необходимости можно вычислить энергетическое содержание в заданных полосах частот, интегрируя квадрат амплитуды спектра. Это полезно для количественной оценки влияния различных частотных компонентов.

Вопрос-ответ:

Как начать поиск спектра сигнала в Mathcad и какие первые шаги необходимо выполнить?

Для начала работы с анализом спектра сигнала в Mathcad необходимо загрузить или создать сигнал в виде массива данных. Затем важно выбрать подходящий метод преобразования, чаще всего используется быстрое преобразование Фурье (FFT). В Mathcad есть встроенные функции, которые позволяют применить FFT к набору числовых значений. После этого можно построить график амплитудного спектра, что даст наглядное представление о частотном составе сигнала.

Какие особенности нужно учитывать при выборе параметров для преобразования Фурье в Mathcad?

Параметры, которые влияют на качество спектрального анализа, включают длину сигнала и частоту дискретизации. Чем больше длина массива данных, тем выше разрешение в частотной области, но увеличивается и вычислительная нагрузка. Частота дискретизации определяет верхнюю границу анализируемых частот (частоту Найквиста). Также стоит обратить внимание на наличие оконных функций, которые уменьшают эффект утечки спектра, если сигнал не является периодическим внутри выборки.

Как интерпретировать полученный спектр сигнала после вычислений в Mathcad?

Спектр сигнала обычно представлен в виде графика амплитуды (или мощности) в зависимости от частоты. Пики на этом графике указывают на присутствие определённых частотных компонент. Важно учитывать масштаб и нормализацию амплитуд, чтобы правильно оценить относительную интенсивность гармоник. Если сигнал содержит шум, спектр может выглядеть более размытым, и тогда для точного анализа полезно применять фильтры или усреднение.

Можно ли в Mathcad анализировать спектр сигнала с непериодическими или шумовыми компонентами, и как это сделать?

Да, Mathcad позволяет анализировать сигналы, содержащие непериодические и шумовые части. В таких случаях преобразование Фурье даст спектр с большим количеством составляющих и более сложной структурой. Чтобы выделить полезные частоты, рекомендуется использовать оконные функции для уменьшения эффекта дискретизации, а также методы сглаживания спектра. Иногда полезно применять фильтрацию во временной области перед анализом, чтобы снизить влияние шумов.

Какие ошибки наиболее часто встречаются при поиске спектра сигнала в Mathcad и как их избежать?

Частыми ошибками являются неправильный выбор длины сигнала, что приводит к низкому разрешению спектра, а также несоответствующая частота дискретизации, из-за чего возникает эффект искажения частот (алиасинг). Также часто забывают применять оконные функции, что вызывает появление дополнительных спектральных линий. Чтобы избежать этих ошибок, важно внимательно проверять параметры входных данных и использовать встроенные средства Mathcad для визуализации и контроля корректности расчетов.

Как шаг за шагом выполнить поиск спектра сигнала в Mathcad?

Для поиска спектра сигнала в Mathcad сначала необходимо определить временной ряд сигнала — это может быть массив значений амплитуды во времени. Затем примените встроенную функцию преобразования Фурье, которая вычисляет частотные составляющие сигнала. В Mathcad это обычно функция FFT (быстрое преобразование Фурье). Поэтапно: 1) Задайте временные данные; 2) Выберите или создайте вектор частот, соответствующий размеру сигнала; 3) Используйте FFT для получения комплексного спектра; 4) Выделите амплитуду или мощность, взяв модуль комплексных чисел; 5) Постройте график амплитуды или мощности относительно частоты. Такой подход позволяет увидеть, какие частоты доминируют в исходном сигнале.