Как написать систему уравнений в mathcad

Mathcad предоставляет мощный инструментарий для моделирования и решения систем уравнений с числовыми и символическими переменными. Основной задачей при работе с Mathcad становится корректное формирование системы, обеспечивающее однозначное решение и последующую визуализацию результатов.

Для построения системы уравнений важно правильно задать переменные и использовать оператор равенства «=». В Mathcad система оформляется через объединение уравнений в вектор или матрицу, что позволяет применять встроенные функции решения, например, solve или root. Каждое уравнение должно быть оформлено с учетом порядка переменных и отсутствия циклических ссылок.

Пошаговый подход включает определение переменных, формулировку уравнений, организацию системы в единую структуру и применение соответствующих методов численного или аналитического решения. Важным моментом является проверка размерности и совместимости уравнений, что предотвращает ошибки при вычислениях.

Данная инструкция ориентирована на пользователей с базовым знанием Mathcad, стремящихся к точному и эффективному созданию систем уравнений для инженерных и научных задач.

Создание системы уравнений в Mathcad: пошаговая инструкция

Откройте новый документ Mathcad и выберите область для ввода уравнений. Для ввода первого уравнения введите его непосредственно в рабочем поле, используя клавиатуру и встроенные операторы Mathcad.

После ввода первого уравнения нажмите Enter для перехода на новую строку. Введите второе уравнение аналогично первому. При необходимости уравнения можно разделять с помощью символа «:=» для определения функций или переменных.

Чтобы объединить уравнения в систему, выделите все уравнения, затем воспользуйтесь функцией «solve» или командой «Оператор системы» (system operator), доступной через меню или вводом с клавиатуры. В Mathcad 15 это функция Given, а в Mathcad Prime – функция Given и оператор Find.

Используйте конструкцию Given, чтобы указать все уравнения системы, и функцию Find для поиска значений неизвестных. Например, задайте Given(уравнение1, уравнение2, ...) и вызовите Find(переменная) для решения.

При вводе уравнений учитывайте правильный синтаксис: знак равенства – для уравнивания, двоеточие «:=» – для присваивания. Следите, чтобы все переменные, используемые в системе, были объявлены или вводились явно.

Для повышения точности решения укажите начальные приближения, если решаете нелинейные системы. Начальные значения задаются через функцию Given или с помощью дополнительных параметров функции Find.

Проверьте корректность системы, подставив найденные решения обратно в уравнения с помощью подстановки. Mathcad автоматически обновит значения при изменении переменных, что позволяет быстро убедиться в правильности решения.

Подготовка рабочей области для ввода системы уравнений

Перед вводом системы уравнений в Mathcad необходимо настроить рабочую область для удобства и точности работы. Выполните следующие шаги:

1. Откройте новый лист Mathcad или создайте новую страницу в текущем проекте для организации уравнений.
2. Установите единицы измерения, если переменные зависят от физических величин. Это делается через меню Units, что позволяет автоматически контролировать размерности.
3. Включите отображение сетки и включите функцию выравнивания элементов для точного позиционирования формул.
4. Подготовьте область ввода с помощью блока уравнений: используйте клавишу = или комбинацию Ctrl+Shift+E для быстрого создания выражения.
5. Распределите уравнения вертикально, оставляя пространство для промежуточных вычислений и комментариев, чтобы избежать визуального нагромождения.
6. Используйте функцию именованных переменных для обозначения каждой неизвестной и параметра, что упрощает последующий ввод и отладку.

Правильная организация рабочей области обеспечивает наглядность и снижает вероятность ошибок при вводе сложных систем уравнений.

Способы ввода алгебраических уравнений в Mathcad

В Mathcad алгебраические уравнения вводятся непосредственно в рабочую область с помощью математического редактора. Для создания уравнения используется сочетание клавиш Ctrl + =, которое переключает курсор в режим ввода математического выражения.

При вводе уравнения необходимо использовать знак равенства = для присваивания значений переменным или знак равенства с двойным нажатием = для обозначения уравнений. Mathcad различает выражения присваивания и уравнения по способу ввода знака равенства.

Для ввода степени применяется клавиша ^, а для индексов – нижний индекс, который можно включить через контекстное меню или комбинацию Ctrl + _. Квадратные и круглые скобки вводятся с клавиатуры напрямую, при этом Mathcad автоматически форматирует вложенность скобок.

Переменные в уравнениях вводятся латинскими или греческими символами, которые доступны в панели символов Mathcad. Для сложных функций и операторов рекомендуется использовать встроенные шаблоны, вызываемые через контекстное меню или вкладку «Математика».

Уравнения можно вводить как в явной форме (например, y = 2*x + 3), так и в неявной (например, y - 2*x - 3 = 0), что важно при решении систем уравнений с помощью встроенных функций Mathcad.

При необходимости многострочных уравнений используют символ переноса строки Shift + Enter, что улучшает читаемость и структурирование системы уравнений.

Для проверки корректности введенного уравнения достаточно просто нажать Enter, после чего Mathcad автоматически вычислит выражение или отобразит ошибку синтаксиса.

Задание параметров и переменных в системе уравнений

В Mathcad параметры и переменные необходимо определять перед построением системы уравнений, иначе программа не сможет корректно интерпретировать выражения. Переменные задаются путем простого присваивания значений или формул, например: x := 5 или y := 2*x + 1. Параметры, не являющиеся переменными, лучше объявлять с фиксированными значениями для упрощения вычислений и повышения читаемости.

Для ввода переменных в системе уравнений используйте имена без пробелов и специальных символов, чтобы избежать синтаксических ошибок. Значения могут быть как числовыми, так и векторными, если система предполагает работу с массивами данных. В случае использования параметров, которые не будут изменяться в процессе решения, их объявление стоит вынести в отдельный блок перед системой, чтобы обеспечить прозрачность кода и удобство редактирования.

Mathcad позволяет создавать условные определения переменных через оператор :=, что особенно полезно для параметрических систем. Важно проверить, что все переменные, участвующие в уравнениях, были объявлены до вызова функции решения. Ошибки в названии переменных или пропущенные определения приводят к сбоям вычислений.

При работе с нелинейными системами рекомендуется задать начальные приближения для переменных, чтобы повысить стабильность численного решения. Это делается путем предварительного присваивания значений переменным до объявления системы уравнений.

Для комплексных переменных и параметров используйте соответствующие типы данных Mathcad, избегая автоматического преобразования типов, чтобы не потерять точность вычислений.

Методы решения линейных систем уравнений в Mathcad

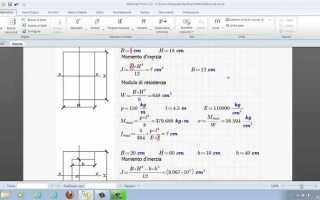
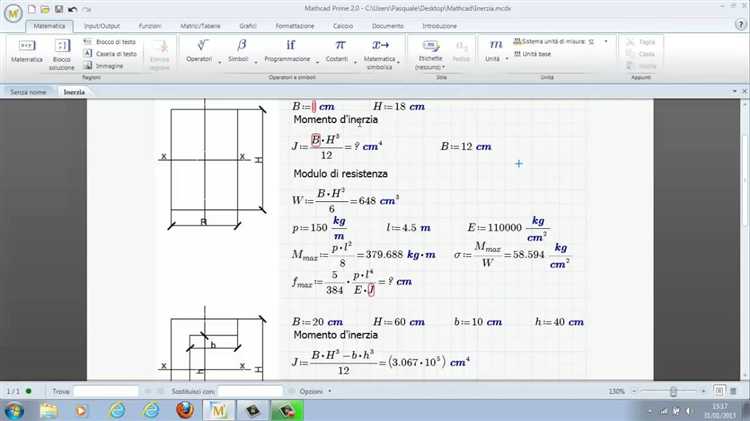
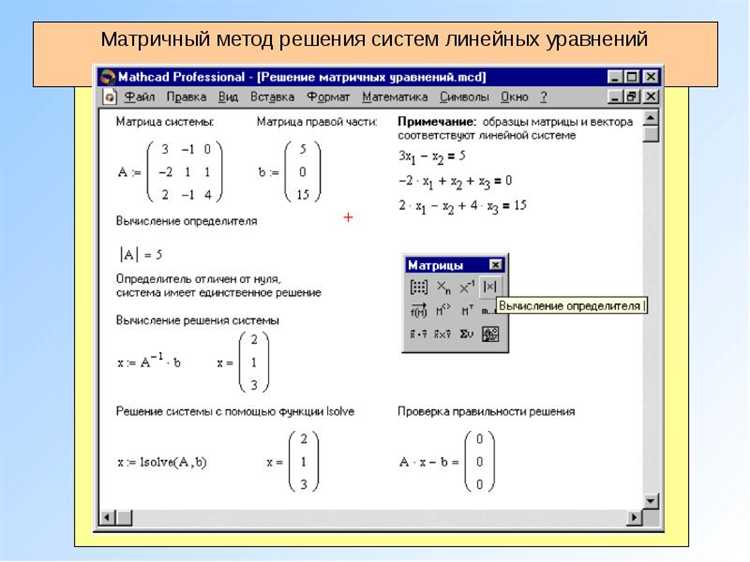
В Mathcad для решения линейных систем уравнений чаще всего применяются два метода: оператор обратной матрицы и функция линейного решения. Для системы вида Ax = b матрица коэффициентов A задается в виде двумерного массива, а вектор свободных членов b – одномерного.

Первый метод – вычисление вектора неизвестных через обратную матрицу: x := A^(-1) * b. При этом необходимо удостовериться, что матрица A невырожденная, иначе Mathcad выдаст ошибку или неверный результат. Проверку можно провести с помощью функции det(A), значение которой не должно быть равно нулю.

Второй, более надежный способ – использование встроенной функции lsolve(A, b), которая автоматически выбирает оптимальный алгоритм решения (LU-разложение или метод Гаусса) без вычисления обратной матрицы. Это повышает точность и производительность при больших системах и плохо обусловленных матрицах.

Для систем с параметрами или с переменными в коэффициентах целесообразно использовать символическое решение через функцию solve(), однако при численном решении предпочтительнее lsolve() из-за быстродействия и устойчивости.

В случаях, когда система содержит более двух уравнений, рекомендуется сначала визуализировать размерность и свойства матрицы A с помощью функций size() и rank(). Если ранг матрицы меньше числа неизвестных, система либо несовместна, либо имеет бесконечное множество решений – Mathcad об этом сообщает, и требуется дополнительный анализ.

Построение графиков решений системы уравнений

Для визуализации решений системы уравнений в Mathcad необходимо определить функции или выражения, которые описывают переменные через независимые параметры. Если система задана явно, следует выделить каждую переменную как функцию от параметра, обычно времени или одной из переменных.

Начните с вычисления численного решения системы с помощью встроенной функции solve() или аналога, задав начальные приближения. После получения численных данных создайте массивы значений для каждой переменной, подставляя значения параметра с нужным шагом.

Для построения графика используйте оператор plot(), передав в качестве аргументов параметры по оси X и соответствующие решения по оси Y. Рекомендуется отдельно строить графики каждой переменной для наглядности, используя функцию multi-plot или объединяя графики на одном полотне с различными цветами и легендами.

Для систем из двух уравнений можно визуализировать траекторию решения на фазовой плоскости, отложив одну переменную по оси X, другую – по оси Y. Это позволяет выявить устойчивость и характер поведения решений.

Обязательно задайте сетку и подписи осей с помощью команд GridOn(), XLabel(), YLabel(), чтобы упростить интерпретацию графиков. Настройте диапазон отображения для исключения лишних данных и улучшения читаемости.

Если решение зависит от параметров, создайте интерактивные слайдеры для изменения значений параметров и динамического обновления графиков. Это значительно упрощает анализ чувствительности и исследование системы.

Отладка и проверка корректности введённых уравнений

После ввода системы уравнений в Mathcad важно сразу убедиться в её корректности. Программа не всегда указывает на логические ошибки, поэтому требуется ручная отладка. Следуйте приведённым шагам.

1. Проверьте единицы измерения. Mathcad чувствителен к размерностям. Если уравнение содержит переменные с несовместимыми единицами (например, метры и секунды в арифметическом сложении), появится ошибка. Для диагностики временно отключите автоматическую проверку размерностей через меню Tools → Worksheet Options → Unit System.
2. Выведите каждое уравнение отдельно. Назначьте переменные числовыми значениями и убедитесь, что левая и правая части равны. Например, если одно из уравнений: F := m·a, задайте m := 5, a := 2, и проверьте F.
3. Используйте оператор solve или Find только после определения всех переменных и уравнений. Если хотя бы одна переменная осталась неопределённой, Mathcad вернёт ошибку.
4. Проверяйте структуру уравнений: каждое должно быть введено через символ равенства = (а не оператор присваивания :=). Для проверки наведите курсор на уравнение – корректное уравнение подсветится синим, а определение – зелёным.
5. Выведите результат каждого уравнения. Mathcad позволяет оценивать значения выражений. Используйте это, чтобы убедиться, что уравнения не содержат бесконечностей, деления на ноль или NaN.
6. При использовании векторов и матриц проверьте размерности: все операции должны быть согласованы. Например, при перемножении матрицы и вектора количество столбцов первой должно совпадать с числом строк второго.
7. Если система нелинейная, задайте начальные приближения для переменных. Без этого Find не сможет найти решение. Используйте guess values рядом с уравнениями и внимательно отслеживайте, как они влияют на результат.

Эти действия позволят быстро выявить и устранить ошибки до попытки численного решения системы.

Экспорт и сохранение результатов решения системы уравнений

Для сохранения результатов решения системы уравнений в Mathcad используйте встроенные функции экспорта данных. После получения численных значений переменных, определите, какие результаты необходимо сохранить – скалярные значения, векторы или матрицы.

Если требуется сохранить только конкретные значения, создайте в рабочем листе отдельный блок с нужными переменными и используйте правый клик мыши → «Сохранить как» → «Текстовый файл». Результаты будут сохранены в виде строки, соответствующей формату представления на экране.

Для сохранения графиков или визуализаций, связанных с решением системы, выделите объект и используйте «Файл» → «Экспорт» → «Графическое изображение». Поддерживаются форматы PNG, BMP, EMF. Рекомендуется использовать EMF для последующего редактирования в векторных редакторах.

Чтобы сохранить весь рабочий процесс, включая систему уравнений, используйте команду «Сохранить как» и выберите формат XMCD или MCDX (в зависимости от версии). Эти форматы сохраняют как входные данные, так и численные результаты.

Рекомендуется регулярно сохранять промежуточные версии документа, добавляя номер ревизии в имени файла, например: system_solution_v3.xmcd. Это снижает риск потери данных и облегчает отслеживание изменений в системе уравнений.

Вопрос-ответ:

Как в Mathcad задать систему линейных уравнений с несколькими переменными?

Для задания системы линейных уравнений в Mathcad необходимо использовать операторы «равно по определению» (:=) и ввод уравнений в виде вектора или матрицы. Сначала создаются выражения для каждого уравнения, затем они объединяются в вектор или матрицу. После этого используется встроенная функция `lsolve`, которой передаётся матрица коэффициентов и вектор свободных членов. В результате Mathcad находит значения переменных, удовлетворяющие всей системе.

Какие ошибки чаще всего возникают при задании системы уравнений в Mathcad?

Одной из наиболее частых ошибок является использование обычного знака равенства (=) вместо оператора определения (:=) при задании выражений. Также пользователи иногда путают порядок переменных или неверно формируют матрицу коэффициентов. Ещё одна типичная ошибка — несогласованность размерностей, когда количество уравнений не соответствует количеству переменных. Mathcad в таком случае выдаёт сообщение об ошибке или не сможет вычислить результат.

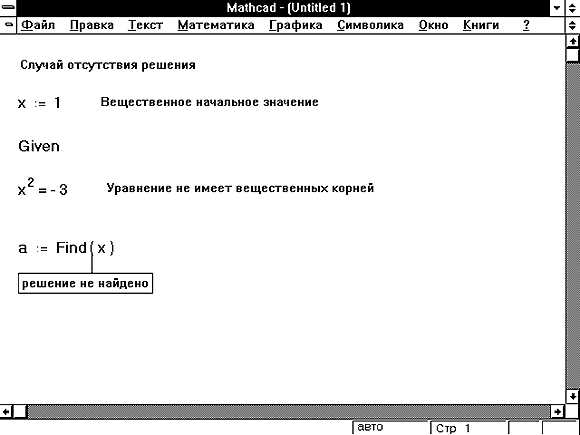
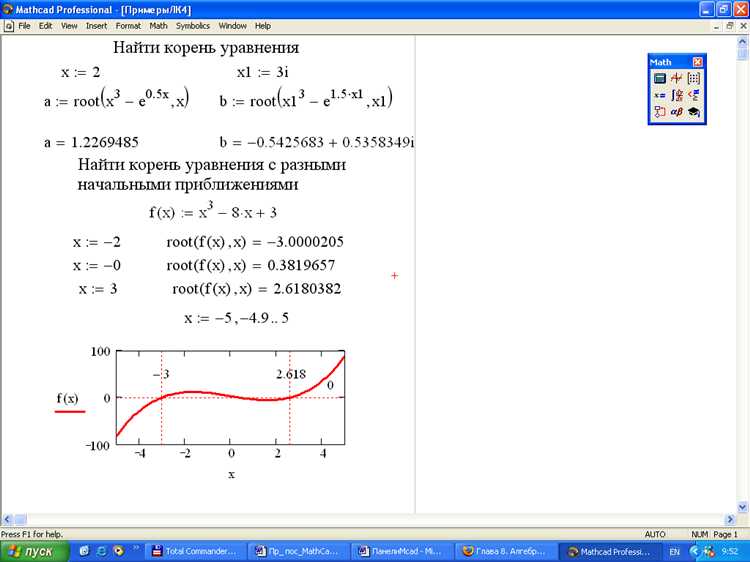
Можно ли в Mathcad решать системы нелинейных уравнений, и если да, то как?

Да, в Mathcad можно решать системы нелинейных уравнений. Для этого применяется функция `root`, либо используется численный решатель с блоком «solve block». Внутри блока переменные и уравнения задаются в явном виде, а затем используется ключевое слово `find`, после чего Mathcad пытается найти численное решение. Такой подход особенно удобен, когда уравнения содержат степенные, тригонометрические или другие нелинейные выражения.

Как в Mathcad задать систему уравнений, если переменные имеют начальные приближения?

Когда используется численный метод решения системы, например через блок «solve block», можно задать начальные приближения переменных с помощью операторов определения. Эти значения указываются перед самим блоком или внутри него и служат отправной точкой для поиска корней. Это особенно актуально для нелинейных систем, где результат зависит от начальных условий, и разные приближения могут приводить к разным решениям или их отсутствию.

Чем отличается задание системы уравнений в Mathcad от аналогичных действий в Excel или Python?

Mathcad ориентирован на математическую запись, максимально приближенную к рукописной. Это позволяет задавать уравнения в привычной форме, не прибегая к программированию. В отличие от Excel, Mathcad автоматически отслеживает единицы измерения и позволяет работать с символьными выражениями. По сравнению с Python, Mathcad проще для пользователей, не знакомых с языками программирования, так как не требует написания кода — всё строится на визуальном вводе формул и данных.