Как вычислить предел в mathcad

Mathcad предоставляет мощный инструмент для аналитического и численного вычисления пределов функций. Для точного результата важно правильно задать выражение и выбрать подходящий метод вычисления, учитывая особенности функции и точку предела.

Первым шагом необходимо определить переменную и функцию, а также задать точку, в которой вычисляется предел. В Mathcad используются встроенные операторы limit(), позволяющие работать как с конечными, так и с бесконечными значениями аргумента.

В процессе вычисления следует учитывать поведение функции слева и справа от точки, если предел существует, они должны совпадать. Mathcad позволяет визуализировать функцию на интервале вокруг точки предела, что помогает выявить особенности и определить тип предела (собственный, бесконечный, или не существующий).

Использование численных методов в Mathcad рекомендуется для сложных функций или когда аналитическое выражение предела невозможно. В статье подробно рассмотрены команды и примеры, которые помогут эффективно и без ошибок вычислить предел в любых стандартных задачах.

Как вычислить предел функции в Mathcad: пошаговая инструкция

Шаг 1. Откройте рабочий лист Mathcad и выберите место для ввода выражения.

Шаг 2. Введите функцию, предел которой требуется найти, например, f(x) := (x^2 — 1)/(x — 1).

Шаг 3. Вставьте оператор предела. Для этого в Mathcad используйте функцию limit(). Синтаксис: limit(выражение, переменная, точка), где выражение – ваша функция, переменная – переменная, по которой берется предел, точка – значение, к которому стремится переменная.

Шаг 4. Например, чтобы вычислить предел функции f(x) при x → 1, введите: limit(f(x), x, 1).

Шаг 5. После ввода нажмите клавишу Enter, Mathcad автоматически вычислит предел и отобразит результат.

Шаг 6. Для проверки предела слева или справа используйте дополнительные параметры в функции limit: limit(f(x), x, 1, ‘left’) или limit(f(x), x, 1, ‘right’).

Шаг 7. Если предел не существует, Mathcad выдаст соответствующее сообщение или покажет знак бесконечности (∞), что указывает на разрыв.

Шаг 8. При работе с бесконечностями задавайте предел при x → ∞, вводя limit(f(x), x, ∞).

Шаг 9. Чтобы избежать ошибок, убедитесь, что функция корректно задана и переменная указана именно та, по которой берется предел.

Подготовка рабочего листа Mathcad для вычисления пределов

Откройте новый лист в Mathcad и сразу задайте единицы измерения, если они важны для задачи. Для точности вычислений перейдите в меню Документ – Настройки вычислений и установите желаемую точность чисел (обычно достаточно 15 значащих цифр).

Создайте область для ввода функции, определив переменную, например, x. Для этого напишите x := и оставьте место для значения или формулы. Это позволит менять переменную динамично в процессе проверки предела.

Вставьте выражение функции, для которой вычисляется предел, используя синтаксис Mathcad. Если функция сложная, лучше разбить её на части, присвоив отдельные подвыражения, что упростит последующую отладку.

Рядом создайте блок для определения точки, в которой нужно найти предел, например, a := значение. Это позволит быстро менять точку без редактирования самой функции.

Подготовьте область для вычисления предела с помощью встроенной функции Mathcad limit(). Введите limit(функция, x, a), где функция, x и a – ранее объявленные выражения.

Для визуального контроля результата рекомендуется рядом вывести график функции в окрестности точки a. Используйте инструмент построения графиков, задавая диапазон значений x около точки предела.

Проверьте, что все переменные и выражения определены без ошибок – Mathcad подсвечивает ошибки автоматически. Если они есть, исправьте их до запуска вычислений.

Ввод функции и определение переменной в Mathcad

Для начала работы с пределом в Mathcad необходимо задать функцию и определить переменную. Переменную вводят напрямую в рабочей области, просто набрав её имя и знак равенства, например, x := 0. Это присваивает переменной значение, необходимое для последующих вычислений.

Функцию вводят с использованием стандартного синтаксиса: имя функции, аргумент в круглых скобках и выражение. Например, f(x) := sin(x) / x. Обязательно использовать двоеточие с равенством := для определения функции.

Mathcad автоматически распознаёт переменную как независимую, если она впервые встречается в определении функции. Для замены переменной достаточно изменить её значение, например, x := 1, и просчитать выражение заново.

Для ввода сложных функций рекомендуется использовать встроенные математические операторы и функции из панели инструментов Mathcad, что минимизирует ошибки в синтаксисе. Скобки играют ключевую роль, поэтому их следует ставить аккуратно, особенно при дробях и степенях.

После определения переменной и функции можно переходить к вычислению пределов, используя соответствующие команды и операторы Mathcad.

Использование встроенной функции limit для вычисления предела

В Mathcad для вычисления предела используется функция limit, которая позволяет определить значение функции при стремлении переменной к заданной точке.

Синтаксис: limit(функция, переменная, точка, направление), где функция – выражение, предел которого требуется найти; переменная – переменная, по которой вычисляется предел; точка – значение, к которому стремится переменная; направление – необязательный параметр, определяющий односторонний предел: + для предела справа, - – слева. Если направление не задано, вычисляется двусторонний предел.

Для вычисления предела в бесконечности в качестве точки указывается ∞ или -∞. Например, limit(x^2/x, x, ∞) вернёт значение бесконечности.

При вводе функции в Mathcad используйте переменные и выражения без пробелов. Для более сложных выражений рекомендуется сначала определить функцию отдельно, затем подставлять её в limit.

Если Mathcad не может найти предел, возвращается символ неопределённости. В таком случае целесообразно исследовать функцию с помощью односторонних пределов, задавая параметр направления.

Встроенная функция limit автоматически учитывает особенности непрерывности и типы разрыва, позволяя вычислять пределы с высокой точностью без необходимости развернутых ручных вычислений.

Настройка направления приближения при вычислении предела

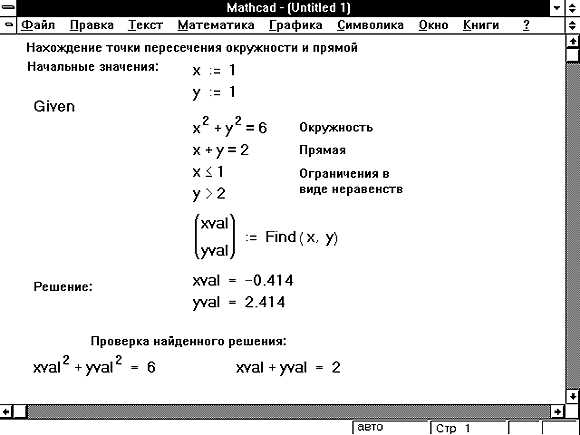
В Mathcad направление приближения к точке при вычислении предела задается с помощью параметра, определяющего с какой стороны функция будет оцениваться: слева, справа или с обеих сторон.

1. Для функции f(x) и точки x = a в выражении предела необходимо использовать дополнительный аргумент, указывающий сторону приближения:
   • +0 – приближение справа (x → a⁺)
   • -0 – приближение слева (x → a⁻)
   • без указания – двустороннее приближение (x → a)
2. В Mathcad команда предела обычно выглядит так: limit(f(x), x, a, d), где d принимает значения +0, -0 или отсутствует.
3. Если требуется вычислить односторонний предел, следует явно прописать параметр d:
   • Пример справа: limit(f(x), x, a, +0)
   • Пример слева: limit(f(x), x, a, -0)
4. Для проверки непрерывности функции с одной стороны рекомендуется сравнить односторонние пределы с значением функции в точке.
5. Если параметр приближения указан неверно или отсутствует при необходимости, Mathcad может вернуть ошибку или некорректный результат.

При вычислениях с бесконечностью параметр направления приближения не применяется, так как пределы определяются только по модулю роста аргумента.

Контроль направления приближения особенно важен для функций с разрывами или кусочно-заданными выражениями, чтобы получить корректные и однозначные значения предела.

Обработка бесконечных пределов и неопределённостей в Mathcad

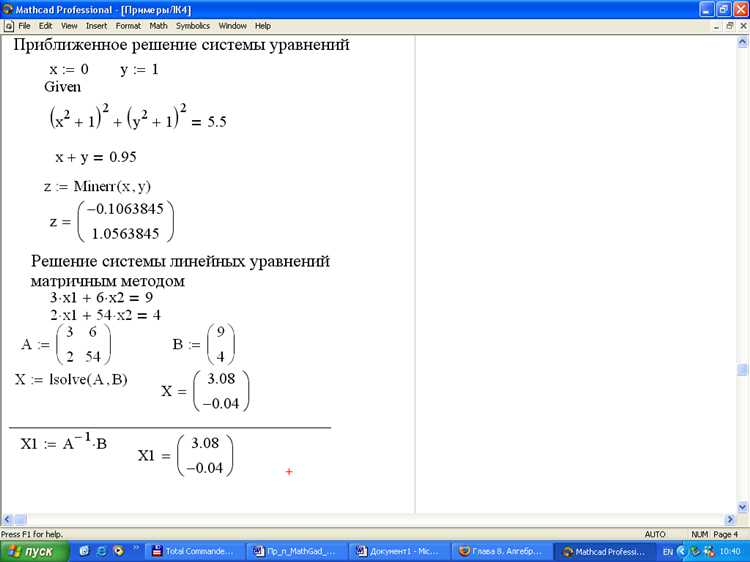
Mathcad позволяет вычислять пределы с бесконечными значениями и неопределённостями, используя встроенные функции и корректное задание выражений. Для бесконечных пределов применяется функция limit(), где аргумент x стремится к ±∞ – в Mathcad обозначается как ∞ или -∞. Например, limit(f(x), x, ∞) вернёт значение предела при x → +∞.

При работе с неопределённостями вида 0/0 или ∞/∞ необходимо преобразовать исходное выражение до вызова limit(). В Mathcad можно использовать алгебраические преобразования или воспользоваться встроенными функциями упрощения, такими как simplify(), чтобы устранить неопределённость. Если преобразование невозможно, можно применять правила Лопиталя вручную, вычисляя производные числителя и знаменателя с помощью diff().

Для вычисления предела с помощью правила Лопиталя алгоритм в Mathcad будет следующим: задать функцию f(x) = числитель / знаменатель, затем определить производные числителя и знаменателя, после чего вызвать limit() для отношения производных при нужном значении x. При необходимости повторять процедуру, если неопределённость сохраняется.

Mathcad корректно обрабатывает бесконечности и неопределённости, если аргументы и функции заданы в допустимых пределах и формате. Важно следить за корректным указанием пределов с использованием символов ∞ или -∞, а также за типом данных – числовой или символический. При численном вычислении, если Mathcad возвращает ошибку, рекомендуется перейти к символическому решению или вручную упростить выражение.

Использование команды limit() совместно с algebraic simplification и дифференцированием обеспечивает точные и надёжные результаты при работе с бесконечными пределами и неопределённостями, что расширяет возможности анализа функций в Mathcad.

Проверка результата и визуализация поведения функции около точки

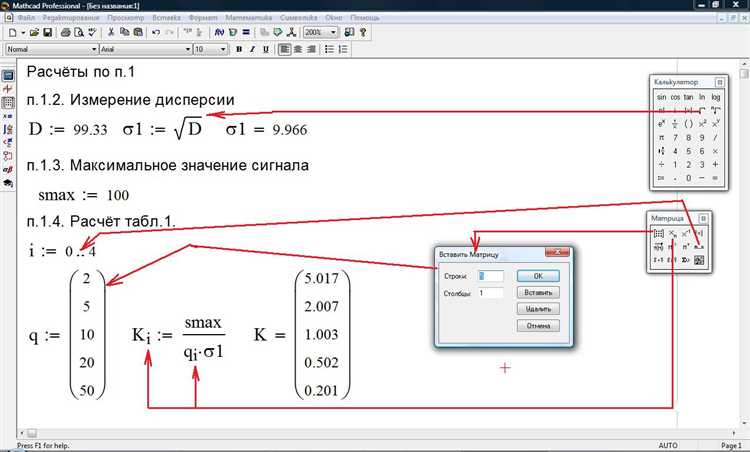
После вычисления предела функции в Mathcad важно убедиться в корректности результата и проанализировать поведение функции в окрестности точки предела. Для этого используется построение графика с увеличением масштаба около заданного значения переменной.

В Mathcad создайте график, добавив зависимость функции от переменной x. Ограничьте область построения так, чтобы ось X охватывала интервал, близкий к точке, в которой вычисляется предел, например, от (a — 0.1) до (a + 0.1), где a – точка предела.

Если предел стремится к бесконечности, используйте логарифмическую шкалу по оси Y для лучшей наглядности. Для конечных пределов рекомендуется сравнить значение функции в точках, близких к a, с вычисленным пределом.

Проверка результата возможна путем вычисления функции в нескольких точках слева и справа от a, а затем сопоставления этих значений с результатом предела. Разрыв или резкий скачок функции укажет на особенности поведения, которые стоит учитывать при интерпретации предела.

Для автоматизации анализа можно создать в Mathcad таблицу с выборочными значениями переменной около точки a и соответствующими значениями функции. Это позволит выявить тенденции и подтвердить правильность вычисленного предела.

Использование численных методов для приближённого вычисления пределов

В Mathcad для приближённого вычисления пределов применяют численные методы, основанные на вычислении значений функции в точках, стремящихся к заданному значению переменной. Для этого создают последовательность аргументов x_n, приближающихся к точке предела, и вычисляют соответствующие значения f(x_n).

Основной шаг – выбор шагов приближения. Рекомендуется брать значения x_n с равномерным убыванием расстояния к точке a: например, a ± 10⁻ⁿ при n = 1, 2, 3. Такой подход позволяет наблюдать поведение функции с двух сторон и выявить односторонние пределы.

В Mathcad удобно использовать встроенные массивы или циклы для автоматического построения таких последовательностей и вычисления значений функции. Для повышения точности вычислений необходимо контролировать числовую стабильность и избегать слишком малых шагов, при которых возникает потеря значимости из-за ограниченной точности вычислений.

Для анализа результатов полезно строить график зависимости f(x_n) от x_n с приближением к точке предела. При визуальном отсутствии разрывов и совпадении значений с обеих сторон можно считать, что численный предел вычислен корректно.

Если функция имеет сложное поведение (осцилляции, разрывы), рекомендуется использовать разностные аппроксимации или метод Ричардсона, уменьшая шаги приближения и анализируя сходимость значений. Mathcad поддерживает численные дифференцирования и аппроксимации, которые облегчают такую проверку.

Ошибки при вычислении пределов и способы их устранения в Mathcad

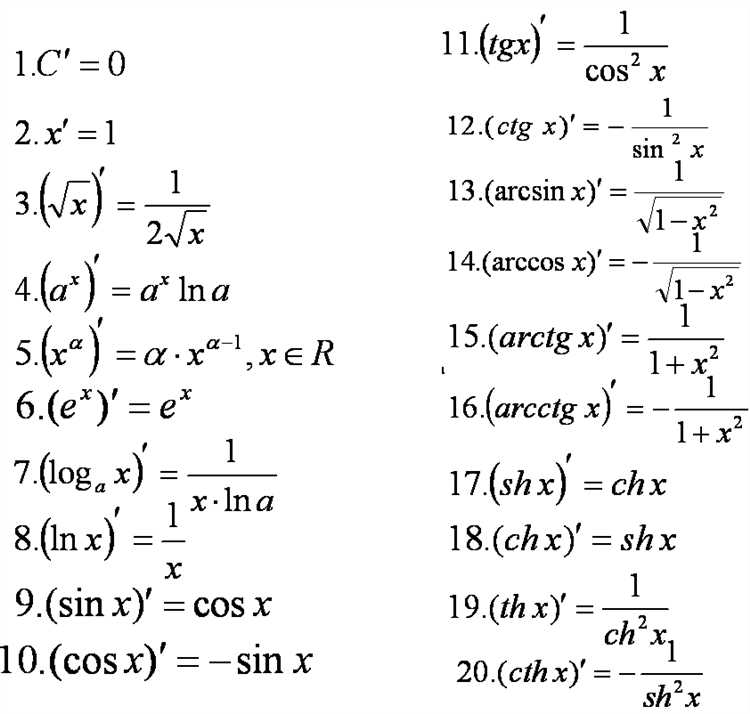
При вычислении пределов в Mathcad часто возникают специфические ошибки, связанные с особенностями синтаксиса и методами обработки функций. Ниже перечислены основные проблемы и практические решения для их устранения.

• Неверный ввод функции или переменной
  • Ошибка: Mathcad не распознает переменную или функцию из-за отсутствия объявления.
  • Решение: обязательно объявляйте все переменные и функции перед вычислением предела. Например, если предел по переменной x, задайте x:= значение или просто используйте x как переменную без конфликтов.
• Некорректное использование оператора предела limit()
  • Ошибка: неверное количество аргументов или неправильный порядок – limit(f(x), x, a).
  • Решение: строго соблюдайте синтаксис: limit(функция, переменная, точка приближения). Проверьте, что функция – выражение, а не значение.
• Пределы с неопределенностями, вызывающие NaN или ошибки вычислений
  • Ошибка: Mathcad возвращает неопределённость или ошибку при прямом вычислении предела с неопределенностями типа 0/0 или ∞/∞.
  • Решение: используйте алгебраические преобразования функции для устранения неопределённости, либо приближайте предел с одной стороны (limit(f(x), x, a, направление)) для определения односторонних пределов.
• Предел в бесконечности
  • Ошибка: неправильное обозначение бесконечности как «∞» вручную приводит к синтаксическим ошибкам.
  • Решение: используйте встроенное обозначение бесконечности, доступное через меню символов Mathcad, или функции, поддерживающие бесконечность. Например, limit(f(x), x, ∞) вводится именно с помощью специального символа, а не текста.
• Числовые ошибки при приближённых вычислениях предела
  • Ошибка: округление и ограничение точности могут искажать результат при численных методах.
  • Решение: включите режим высокой точности вычислений в настройках документа, используйте символическое вычисление (если доступно) или аналитические преобразования для точных результатов.
• Отсутствие определения предела из-за несоответствия типа функции
  • Ошибка: попытка вычислить предел неаналитической или разрывной функции без уточнения направления.
  • Решение: уточняйте направление предела (справа или слева) в параметрах limit, если функция разрывна в точке, либо разбивайте вычисление на интервалы с непрерывной функцией.

Применение этих рекомендаций помогает избежать большинства типичных ошибок и добиться корректного вычисления пределов в Mathcad.

Вопрос-ответ:

Как в Mathcad задать функцию для вычисления предела?

В Mathcad нужно сначала определить функцию через выражение с переменной, например, f(x) := выражение. После этого можно использовать встроенную команду для пределов или воспользоваться численным приближением, подставляя значения x, стремящиеся к нужной точке. Функция должна быть корректно задана, чтобы вычисление было корректным.

Какие шаги нужно выполнить, чтобы найти предел функции в Mathcad?

Сначала создайте определение функции с помощью оператора «:=». Затем используйте специальный инструмент для пределов, который находится в разделе математических функций, указав переменную и точку, к которой стремится аргумент. Если автоматического вычисления нет, можно построить таблицу значений функции при приближении аргумента к точке предела и проанализировать результат.

Можно ли вычислить предел функции в Mathcad, если он не существует в обычном смысле?

Mathcad может не всегда распознавать пределы, которые расходятся или не существуют. В таких случаях лучше исследовать поведение функции около точки приближения вручную — построить график или рассчитать значения функции с разных сторон. Это поможет понять, есть ли предел и как он себя ведет.

Какой формат записи результата предела в Mathcad считается корректным?

Результат предела обычно выводится как числовое значение или символическое выражение, если Mathcad смог вычислить его точно. При численном методе результатом будет приближённое число с указанной точностью. При невозможности вычислить предел автоматически, вывод может содержать условное обозначение или ошибку.

Что делать, если Mathcad не вычисляет предел автоматически?

Если автоматическое вычисление не срабатывает, можно попробовать упростить функцию вручную, разложить её в ряд, изменить переменную или использовать приближённые вычисления, подставляя значения близко к точке предела. Также полезно проверить корректность введённой функции и области определения.

Как в Mathcad найти предел функции в точке, если он существует?

В Mathcad для вычисления предела функции в конкретной точке нужно использовать встроенную функцию limit(). Сначала задайте выражение функции, затем вызовите limit(функция, переменная, значение), где переменная — это переменная функции, а значение — точка, к которой стремится переменная. Например, limit(sin(x)/x, x, 0) вычислит предел функции sin(x)/x при x, стремящемся к нулю. Если предел существует, Mathcad выдаст числовое значение. Если нет — появится сообщение об ошибке или неопределённость.