В задачах, связанных с моделированием случайностей – от игровых механик до симуляции процессов – часто требуется задать вероятность наступления определённых событий. В Python такую механику можно реализовать несколькими способами, каждый из которых подходит под разные сценарии: фиксированный список вероятностей, динамическое перераспределение весов, применение нормального или другого распределения.
Для базового случая с фиксированными шансами достаточно использовать функцию random.choices() из стандартного модуля random. Она позволяет задать список событий и список соответствующих им весов. Например: random.choices(['успех', 'неудача'], weights=[0.7, 0.3]). Здесь вероятность успеха составляет 70%, а неудачи – 30%.
Если веса событий могут изменяться во времени, удобнее использовать словарь с настраиваемыми значениями. После пересчёта весов требуется их нормализовать, чтобы сумма составляла 1. Это особенно важно при работе с собственными алгоритмами, где используется random.uniform(0, 1) и ручное определение порогов выпадения событий.
При необходимости симулировать неравномерное распределение (например, редкие события с малым шансом) можно использовать логарифмическое или экспоненциальное распределение из модуля numpy.random. Пример: numpy.random.exponential(scale=1.0) для генерации редких, но возможных событий.
Отдельного внимания требует контроль воспроизводимости. Для этого следует использовать random.seed() или numpy.random.seed(), чтобы генерация случайностей была детерминированной при одинаковом начальном значении. Это важно при тестировании или отладке логики выпадения событий.
Как задать вероятность для событий с разным весом
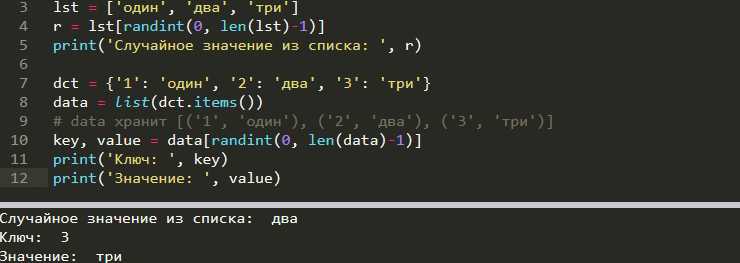
Для задания вероятностей событий с неравными шансами используют веса. В Python это удобно реализуется через функцию random.choices из модуля random. Список событий передаётся в аргумент population, соответствующие веса – в weights.
Пример: пусть события A, B и C имеют веса 10, 30 и 60 соответственно. Тогда вызов random.choices(['A', 'B', 'C'], weights=[10, 30, 60], k=1) вернёт одно событие с учётом указанных пропорций. Параметр k задаёт количество выбираемых элементов.
Для нормализации вручную: сумма всех весов должна быть положительной. Если указать вероятности в долях, например [0.1, 0.3, 0.6], результат будет тем же. Функция автоматически приведёт их к относительным значениям.
Если события привязаны к числовым диапазонам, например при генерации случайных чисел с неравномерной плотностью, веса можно использовать как длины интервалов. Тогда выбирается диапазон по весу, после чего случайное значение извлекается уже из него. Это реализуется через накопленные суммы и функцию bisect.
Для контроля повторяемости результатов нужно установить фиксированный seed с помощью random.seed.
В NumPy аналогичная возможность реализована через numpy.random.choice с аргументом p, в который передаётся список вероятностей. Он должен быть нормализован: сумма значений – 1.
Использование random.choices для выбора с учетом вероятностей
Функция random.choices из стандартного модуля random позволяет выбирать элементы из последовательности с заданными весами. Это удобно при моделировании событий с неравномерным распределением вероятностей.
- Синтаксис:
random.choices(population, weights=None, k=1) population– список возможных значений.weights– список весов, соответствующих элементамpopulation.k– количество элементов в результате.
Вес не обязан быть в пределах от 0 до 1, допускаются любые положительные числа. Вероятность каждого элемента вычисляется как его вес, делённый на сумму всех весов.
import random
события = ['успех', 'неудача']
веса = [0.7, 0.3]
результат = random.choices(события, weights=веса, k=1)[0]
При необходимости можно использовать k > 1 для генерации выборки:
выборка = random.choices(события, weights=веса, k=1000)
Для получения частот рекомендуется использовать collections.Counter:
from collections import Counter
статистика = Counter(выборка)
Если не указать weights, элементы будут выбираться с равными шансами. Чтобы избежать ошибок, длина списка весов должна совпадать с длиной списка значений.
Функция random.choices подходит для моделирования событий с повторением. Для выборки без повторов следует использовать random.sample, но она не поддерживает веса.
Реализация выпадения события с заданным шансом вручную
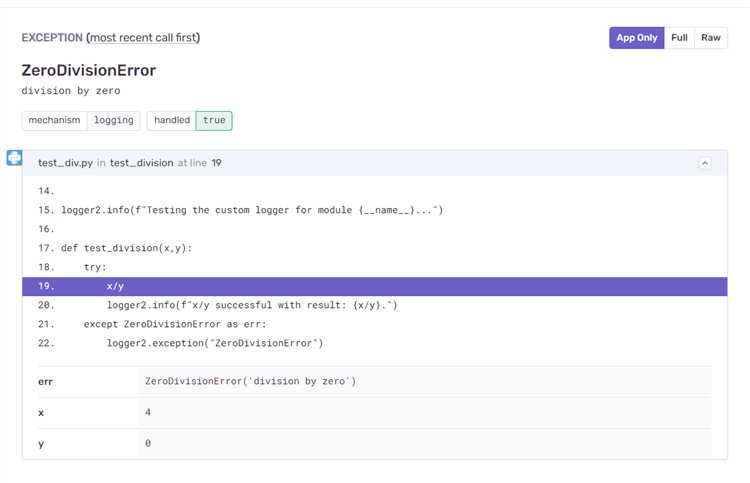
Для ручной реализации выпадения события с фиксированной вероятностью достаточно использовать генератор случайных чисел и логическое сравнение. Допустим, шанс события – 30%. Это означает, что событие должно происходить в 30 из 100 случаев.
Пример кода:
import random
def событие_произошло(шанс_в_процентах):
return random.randint(1, 100) <= шанс_в_процентах
# Пример использования
if событие_произошло(30):
print("Событие произошло")
else:
print("Событие не произошло")
Пояснение: функция random.randint(1, 100) возвращает целое число от 1 до 100 включительно. Если оно меньше или равно значению заданного шанса, считается, что событие произошло.
Рекомендации:
- Избегайте использования random.random() с округлением, так как это снижает точность.
- Для дробных значений, например 2.5%, используйте диапазон с большим числом грануляции, например от 1 до 1000:
def событие_произошло(шанс_в_процентах):
return random.randint(1, 1000) <= шанс_в_процентах * 10
Такой подход даёт точность до десятой доли процента без потерь в читаемости кода.
Создание таблицы выпадений для дискретных вероятностей
Для моделирования случайных событий с заданными дискретными вероятностями удобно использовать таблицу выпадений, представленную в виде диапазонов чисел, соответствующих каждому событию. Это позволяет быстро сопоставить случайное число из равномерного распределения с нужным исходом.
Сначала нужно нормализовать вероятности так, чтобы их сумма равнялась единице. Затем каждую вероятность можно преобразовать в числовой диапазон в пределах, например, от 1 до 1000. Если вероятность события A равна 0.25, оно получит диапазон из 250 значений. Далее суммируются длины всех диапазонов, и каждому событию присваиваются подряд идущие отрезки.
Пример кода:
import random
events = {
"A": 0.25,
"B": 0.50,
"C": 0.15,
"D": 0.10
}
scale = 1000
table = []
current = 1
for event, prob in events.items():
count = int(prob * scale)
table.append((range(current, current + count), event))
current += count
def roll():
r = random.randint(1, scale)
for rng, event in table:
if r in rng:
return event
Функция roll возвращает случайное событие в соответствии с заданными вероятностями. Величина scale определяет точность: при значении 1000 минимальная возможная вероятность – 0.001. При необходимости можно увеличить масштаб, чтобы поддерживать более мелкие доли.
Имитация редких событий с плавающим шансом
Редкие события с изменяемой вероятностью возникают в случаях, когда шанс зависит от внешних условий или предыдущих попыток. Типичный пример – система "pity" в играх, где вероятность увеличивается при неудачных попытках.
Для моделирования используется функция с динамическим шансом. Пример: вероятность события увеличивается на 1% после каждой неудачи, начиная с 1% и ограниченная максимумом в 10%.
import random
def rare_event_with_ramp(base=0.01, step=0.01, cap=0.10, attempts=100):
chance = base
for i in range(1, attempts + 1):
if random.random() <= chance:
print(f"Событие произошло на попытке {i} с шансом {chance:.2%}")
return i
chance = min(chance + step, cap)
print("Событие не произошло")
return None
rare_event_with_ramp()
Такой подход позволяет управлять ожиданием: при фиксированной вероятности 1% событие произойдёт в среднем на 69-й попытке. При наращивании шанса среднее число попыток снижается. Поведение можно точно оценить симуляцией.
def simulate(n=10000):
results = []
for _ in range(n):
result = rare_event_with_ramp()
if result:
results.append(result)
average = sum(results) / len(results)
print(f"Среднее количество попыток: {average:.2f}")
simulate()
Плавающий шанс позволяет контролировать распределение вероятностей и снижает дисперсию. Это особенно важно, когда редкое событие должно гарантированно происходить в течение ограниченного числа попыток.
Проверка корректности распределения через симуляции

Для проверки корректности распределения событий в Python можно использовать симуляции, которые позволяют на практике оценить, насколько теоретические расчеты совпадают с реальными результатами. Этот подход полезен при моделировании случайных процессов, где теоретические предположения могут не всегда точно отражать реальные данные.
Шаги для выполнения симуляции:
- Определение модели распределения: Для начала нужно выбрать тип распределения, который будет симулироваться, например, равномерное, нормальное или биномиальное распределение. Каждый тип распределения имеет свои особенности, которые важно учесть при моделировании.
- Генерация случайных чисел: В Python для генерации случайных значений можно использовать модуль
randomилиnumpy.random. Например, для равномерного распределения от 0 до 1 можно использоватьrandom.uniform(0, 1), а для нормального –numpy.random.normal(mu, sigma, size). - Проведение симуляции: Создайте цикл, который многократно генерирует случайные значения согласно выбранному распределению. Например, для оценки равномерного распределения можно выполнить генерацию 10 000 чисел и подсчитать их распределение по интервалам.
- Сравнение теоретического и фактического распределений: Полученные результаты симуляции нужно сравнить с теоретическими значениями. Например, для равномерного распределения можно проверить, что все интервалы имеют примерно одинаковую частоту появления чисел.
- Оценка статистической погрешности: Для оценки точности симуляции можно использовать статистические методы, такие как вычисление стандартного отклонения или проведение теста согласия (например, теста хи-квадрат). Эти методы позволяют количественно оценить отклонение полученных результатов от теоретической модели.
Пример кода для проверки равномерного распределения:
import random
import matplotlib.pyplot as plt
# Генерация 10 000 случайных чисел с равномерным распределением
samples = [random.uniform(0, 1) for _ in range(10000)]
# Визуализация гистограммы
plt.hist(samples, bins=50, density=True)
plt.title('Гистограмма случайных чисел')
plt.show()
Этот код генерирует 10 000 чисел с равномерным распределением от 0 до 1 и строит гистограмму, которая визуально демонстрирует, насколько равномерно распределены числа. Результаты должны быть примерно симметричными по отношению к центральному значению, если распределение корректно.
Для более сложных распределений, таких как нормальное или биномиальное, нужно будет использовать соответствующие функции из библиотеки numpy и более сложные методы визуализации и анализа.
Проверка через симуляции позволяет выявить проблемы с моделью или ошибками в коде, что делает этот метод полезным инструментом для проверки теоретических предположений в реальных условиях.
Интеграция вероятностного выбора в игровую механику
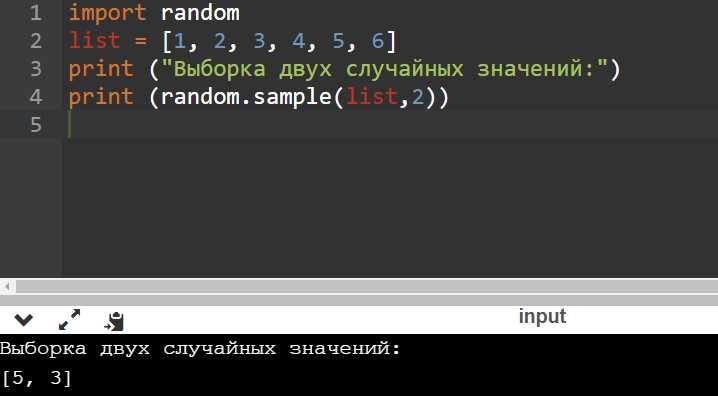
В игровых приложениях вероятностный выбор применяется для создания элементов случайности, которые влияют на ход игры, такие как выпадение предметов, шанс на успешное действие персонажа или случайные события. В Python для моделирования вероятностных событий часто используется стандартный модуль random, который позволяет легко интегрировать случайные элементы в игровую механику.
Одним из наиболее популярных методов является использование функции random.choice(), которая выбирает случайный элемент из списка, или random.random(), генерирующей случайное число от 0 до 1. Например, для симуляции выпадения редких предметов можно задать вероятность 10% для каждого предмета, создавая условие, при котором этот предмет выпадает только при генерации числа меньше 0.1.
Для более сложных сценариев, где важно учитывать несколько факторов или многократные выборы, можно использовать функцию random.choices(), которая позволяет задать веса для элементов. Это особенно полезно, если, например, шанс выпадения разных объектов или событий должен зависеть от уровня игрока или других динамических факторов в игре.
Важной частью интеграции вероятностных механизмов является правильная настройка весов и вероятностей. Например, при создании механики, где игроки могут столкнуться с случайными врагами или событиями, можно использовать распределение вероятностей, которое учитывает текущий прогресс игрока. Один из подходов – использование экспоненциального или нормального распределения для создания более плавных и динамичных изменений вероятностей.
Механики с вероятностным выбором также активно применяются в квестах, где исход зависит от случайных решений, и в мини-играх, где элементы случайности создают интересные и неожиданные моменты. Важно понимать, что случайность не должна делать игру слишком непредсказуемой. Игрок должен чувствовать, что его действия влияют на результаты, но случайность при этом добавляет элемент неожиданности и интереса.
Для тестирования вероятностных систем важно учитывать большие выборки, чтобы результаты случайных процессов не создавали слишком сильных отклонений от ожиданий. Модуль random в Python предоставляет достаточно гибкости для реализации сложных вероятностных механизмов, которые можно адаптировать под конкретные нужды игры.
Вопрос-ответ:
Как с помощью Python рассчитать вероятность выпадения события?
Для расчета вероятности события в Python можно использовать стандартные математические функции. Если речь идет о простом случае, например, подбрасывания монеты, вероятность выпадения "орел" будет равна 0.5. Для более сложных ситуаций можно применить библиотеки, такие как `random` или `numpy`, которые позволяют моделировать случайные события и вычислять вероятность на основе их частоты.
Что такое шанс выпадения события в контексте программирования на Python?
Шанс выпадения события в программировании означает вероятность того, что событие произойдёт при случайных условиях. В Python для моделирования случайных событий используется модуль `random`. Например, чтобы вычислить вероятность выпадения определенного числа на кубике, можно сгенерировать случайное число и подсчитать, как часто оно совпадает с нужным значением. Пример: для шестигранного кубика шанс выпадения определённого числа составляет 1/6.
Какие библиотеки Python могут помочь при моделировании вероятностных событий?
Для моделирования вероятностных событий в Python часто используют библиотеки `random` и `numpy`. Модуль `random` предоставляет функции для генерации случайных чисел, таких как `random.randint()` для целых чисел или `random.random()` для чисел с плавающей запятой. Библиотека `numpy` дополнительно предлагает более сложные функции для работы с массивами и распределениями, например, `numpy.random.choice()` для случайного выбора элементов из массива.
Можно ли использовать Python для оценки шансов на основе реальных данных?
Да, Python отлично подходит для оценки вероятности на основе реальных данных. Для этого можно использовать библиотеки, такие как `pandas` для обработки данных и `scipy` для статистических расчетов. С помощью этих инструментов можно анализировать данные, например, вычислять частоту появления определённых событий и на основе этого оценивать их вероятность. Также для более точных расчетов могут быть использованы методы статистической регрессии и теоремы Байеса.