Корреляция – это статистическая мера, которая помогает понять, как две переменные соотносятся между собой. В Python для этого существует несколько методов, среди которых наиболее популярны функции из библиотеки Pandas и NumPy. Они позволяют быстро вычислить коэффициент корреляции для различных типов данных, будь то числовые или категориальные переменные. Важно понимать, что корреляция не означает причинно-следственную связь, а лишь выявляет степень и направление взаимосвязи.
Для вычисления корреляции можно использовать метод corr() в Pandas. Он позволяет посчитать корреляцию Пирсона по умолчанию, но также есть возможность рассчитать другие типы корреляции, такие как Спирмена или Кендалла, для разных типов данных. Для этого достаточно указать соответствующий параметр в методе. При анализе данных важно учитывать, что корреляция Пирсона хорошо работает для линейных зависимостей, в то время как для нелинейных зависимостей стоит использовать другие методы.
Пример: чтобы посчитать корреляцию между двумя колонками в датафрейме Pandas, достаточно выполнить вызов df[‘column1’].corr(df[‘column2’]). Этот простой метод позволяет за считанные секунды получить результат, который можно использовать для дальнейшего анализа.
Еще один популярный способ – использование библиотеки NumPy для вычисления коэффициента корреляции Пирсона через функцию numpy.corrcoef(). Это дает более гибкие возможности для работы с массивами данных. Однако для удобства в анализе больших наборов данных лучше всего использовать Pandas, так как эта библиотека предоставляет дополнительные возможности для предварительной обработки и визуализации данных.
Подготовка данных для расчета корреляции в Python
Перед расчетом корреляции в Python необходимо убедиться, что данные подготовлены должным образом. Неправильная структура данных может привести к искаженным результатам. Рассмотрим шаги подготовки данных, которые гарантируют корректность анализа.
- Проверка типов данных. Все переменные, для которых будет вычисляться корреляция, должны быть числовыми. Для этого можно использовать метод
dtypesбиблиотеки Pandas:
import pandas as pd
data = pd.read_csv('data.csv')
print(data.dtypes)Если в наборе данных есть категориальные признаки, их следует исключить или преобразовать в числовые. Например, категориальные признаки можно закодировать через pd.get_dummies().
- Обработка пропусков. Недостающие значения могут привести к ошибкам при расчете корреляции. Пропуски следует либо удалить, либо заменить. Для удаления строк с пропусками используется метод
dropna(), а для замены –fillna():
data = data.dropna() # удаление строк с пропусками
data = data.fillna(0) # замена пропусков на 0В случае, если пропусков много, рекомендуется использовать методы, такие как медианная или средняя замена, которые сохраняют распределение данных.
- Проверка на выбросы. Наличие экстремальных значений может значительно исказить корреляцию. Чтобы обнаружить выбросы, можно использовать методы визуализации, такие как коробчатые диаграммы, или расчет Z-оценки. Для удаления выбросов можно использовать фильтрацию данных:
from scipy.stats import zscore
data = data[(zscore(data) < 3).all(axis=1)] # удаление выбросов, Z-оценка больше 3- Нормализация данных. Корреляция чувствительна к масштабу переменных. Если данные имеют разные масштабы, их необходимо привести к одному. Для этого используется стандартная нормализация или мин-макс масштабирование. В библиотеке
sklearnдоступны инструменты для этого:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)Если же нужно привести данные к интервалу от 0 до 1, можно использовать MinMaxScaler.
- Корреляция между переменными. Важно удостовериться, что анализируются только те переменные, которые имеют смысл для расчета корреляции. Часто корреляцию считают только между числовыми переменными, так как для категориальных данных используются другие методы, например, коэффициент контингенции или коэффициент Хи-квадрат.
Эти шаги позволяют подготовить данные к расчёту корреляции в Python и избежать ошибок, связанных с неправильной структурой данных. Только после выполнения этих процедур можно приступать к анализу, рассчитывая корреляционные матрицы или пары корреляций между переменными.
Использование библиотеки Pandas для вычисления корреляции
Для вычисления корреляции между переменными в Python часто используется библиотека Pandas. Это позволяет быстро и эффективно анализировать связи между различными столбцами в DataFrame. Pandas предоставляет функцию corr(), которая автоматически рассчитывает корреляцию для числовых данных.
Функция corr() по умолчанию использует метод Пирсона для вычисления линейной корреляции между столбцами. Она возвращает матрицу корреляции, где значения варьируются от -1 до 1, где -1 означает полную отрицательную зависимость, 1 – полную положительную зависимость, а 0 – отсутствие линейной зависимости.
Пример использования:
import pandas as pd
# Создание DataFrame
data = {'A': [1, 2, 3, 4, 5],
'B': [5, 4, 3, 2, 1],
'C': [2, 3, 4, 5, 6]}
df = pd.DataFrame(data)
# Расчет корреляции
correlation_matrix = df.corr()
print(correlation_matrix)Этот код создаст DataFrame с тремя столбцами и затем вычислит корреляцию между ними. Результатом будет матрица, которая помогает понять, как связаны данные в каждом столбце.
Для использования других методов корреляции, например, Спирмена или Кендала, можно передать параметр method в функцию corr():
correlation_spearman = df.corr(method='spearman')
correlation_kendall = df.corr(method='kendall')Метод Спирмена подходит для оценки монотонных зависимостей, а Кендалл – для более устойчивых оценок в случае небольших наборов данных. Каждый из методов имеет свои особенности и выбирается в зависимости от типа данных и исследуемых взаимосвязей.
Важно учитывать, что функция corr() работает только с числовыми данными. Если в DataFrame присутствуют категориальные данные, их необходимо предварительно преобразовать в числовые значения, например, с помощью кодирования или преобразования в порядковые данные.
Также стоит помнить, что корреляция не всегда означает причинно-следственную связь. Высокая корреляция может быть следствием третьего фактора, не учитываемого в модели.
Типы корреляций: Пирсона, Спирмена и Кендала
Корреляция измеряет степень взаимосвязи между двумя переменными. В Python для расчета корреляции часто используют три основных метода: Пирсона, Спирмена и Кендала. Каждый из этих методов имеет свои особенности и области применения.
Корреляция Пирсона (Pearson) – это наиболее часто используемый метод, который предполагает линейную зависимость между переменными. Он измеряет, насколько сильно изменение одной переменной связано с изменением другой. Пирсон применяется, когда данные распределены нормально, и отношения между переменными линейны. Этот метод может быть чувствителен к выбросам, которые могут существенно повлиять на результат.
Корреляция Спирмена (Spearman) оценивает монотонные зависимости между переменными. В отличие от Пирсона, Спирмен не требует нормальности распределения и линейности связи, что делает его более универсальным для различных типов данных. Этот метод работает с рангами значений и подходит для анализа данных с порядковой шкалой или когда связь между переменными не является линейной.
Корреляция Кендала (Kendall) также используется для оценки монотонных зависимостей, но отличается от Спирмена способом расчета. Кендала считается более устойчивым к выбросам и может давать более точные результаты при анализе малых выборок. Он основывается на сравнении пар значений и учитывает количество согласованных и несогласованных пар. Этот метод чаще применяется при анализе небольших наборов данных или когда нужно повысить точность корреляции в условиях неопределенности.
Выбор метода зависит от характера данных и целей анализа. Если данные подчиняются нормальному распределению и предполагается линейная зависимость, то метод Пирсона будет наиболее подходящим. Для данных с монотонными, но не линейными зависимостями лучше использовать корреляцию Спирмена. Если же требуется высокая устойчивость к выбросам и точность при небольших выборках, то оптимальным выбором будет корреляция Кендала.
Как интерпретировать коэффициент корреляции
Когда коэффициент корреляции равен 1, это указывает на идеальную положительную линейную зависимость: увеличение одной переменной ведет к пропорциональному увеличению другой. В случае значения -1 наблюдается идеальная отрицательная линейная зависимость: увеличение одной переменной ведет к пропорциональному уменьшению другой.
Значение, близкое к 0, свидетельствует об отсутствии линейной зависимости между переменными. Важно помнить, что коэффициент корреляции измеряет только линейные отношения, и при его низких значениях могут существовать нелинейные зависимости, которые он не фиксирует.
Значения коэффициента корреляции могут быть интерпретированы следующим образом:
- 0.9 и выше: очень сильная корреляция
- от 0.7 до 0.9: сильная корреляция
- от 0.5 до 0.7: умеренная корреляция
- от 0.3 до 0.5: слабая корреляция
- менее 0.3: очень слабая или отсутствующая корреляция.
При интерпретации важно учитывать контекст данных. Например, даже коэффициент корреляции 0.8 в области медицины может означать достаточно сильную связь, в то время как в экономике такая зависимость может быть недостаточно убедительной для принятия решений.
Для полноценной оценки стоит также учитывать визуальные инструменты, такие как диаграммы рассеяния, которые могут показать возможное наличие закономерностей, которые коэффициент корреляции не всегда может выявить.
Корреляция между числовыми и категориальными переменными
Пример использования ANOVA для определения, влияет ли категориальная переменная (например, тип продукта) на стоимость товара, будет следующим:
from scipy import stats
import pandas as pd
# Пример данных
data = {'Product': ['A', 'B', 'A', 'B', 'C', 'C', 'A'],
'Price': [100, 200, 150, 250, 300, 350, 120]}
df = pd.DataFrame(data)
# Группировка данных по категориям и применение ANOVA
groups = [df[df['Product'] == category]['Price'] for category in df['Product'].unique()]
f_statistic, p_value = stats.f_oneway(*groups)
print(f'F-статистика: {f_statistic}, P-значение: {p_value}')
Кроме того, можно использовать коэффициент корреляции Крамера (Cramér's V) для оценки силы связи между категориальной и числовой переменной. Этот метод хорошо работает в случае, когда категориальная переменная имеет несколько уровней, и требуется измерить силу ассоциации между переменными. В Python для этого используется библиотека association-metrics, которая предлагает удобные функции для вычисления Cramér's V.
Пример вычисления Cramér's V для таблицы сопряженности:
from association_metrics import cramers_v
# Пример данных
data = {'Category': ['A', 'B', 'A', 'B', 'A', 'C'],
'Value': [100, 200, 150, 250, 180, 300]}
df = pd.DataFrame(data)
# Создание таблицы сопряженности
contingency_table = pd.crosstab(df['Category'], df['Value'])
# Вычисление Cramér's V
cramers_value = cramers_v(contingency_table)
print(f'Коэффициент корреляции Крамера: {cramers_value}')
Коэффициент близкий к 0 указывает на слабую связь между переменными, в то время как значения, близкие к 1, указывают на сильную связь.
Для категориальных переменных, состоящих из порядковых категорий, можно использовать метод ранговой корреляции Спирмена, который оценивает зависимость между ранговыми значениями переменных. Это особенно полезно, когда категориальная переменная имеет порядок (например, низкий, средний, высокий). Функция spearmanr из библиотеки scipy позволяет вычислить этот коэффициент.
Понимание корреляции между числовыми и категориальными переменными помогает выявить скрытые зависимости и строить более точные модели для анализа данных. Выбор метода зависит от типа категориальных данных и целей исследования, а также от того, требуется ли учитывать порядок категорий или только их принадлежность к группам.
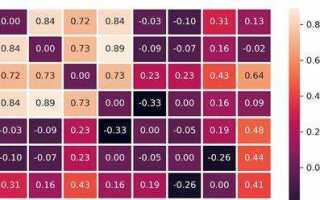
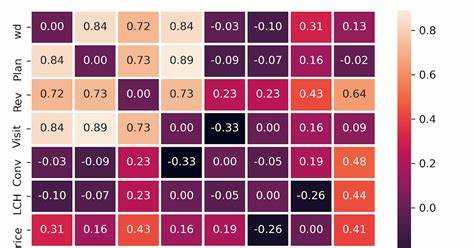
Построение тепловой карты корреляции в Python
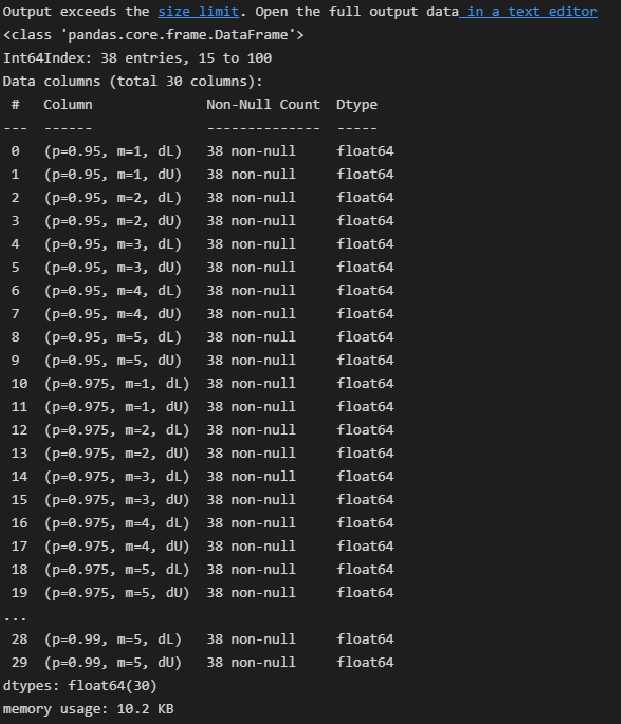
Для начала необходимо рассчитать корреляцию между переменными. Используется метод corr() из библиотеки Pandas, который вычисляет коэффициент Пирсона, показывающий степень линейной зависимости между переменными. Этот коэффициент варьируется от -1 (полная отрицательная корреляция) до +1 (полная положительная корреляция), где 0 означает отсутствие линейной зависимости.
Пример расчета корреляции и построения тепловой карты:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Загрузка данных
data = pd.read_csv('data.csv')
# Рассчитываем корреляцию
correlation_matrix = data.corr()
# Строим тепловую карту
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5)
plt.title('Тепловая карта корреляции')
plt.show()
Ключевые параметры для настройки визуализации:
annot=True– отображает численные значения корреляции на тепловой карте.cmap='coolwarm'– выбирает цветовую палитру, где теплые цвета (красные) означают положительную корреляцию, а холодные (синие) – отрицательную.fmt='.2f'– задает формат отображения чисел (до двух знаков после запятой).linewidths=0.5– добавляет разделительные линии между клетками, улучшая читаемость.
Тепловая карта позволяет визуально определить переменные с высокой и низкой корреляцией. Например, если два признака имеют значение корреляции близкое к 1 или -1, это означает сильную зависимость. Для лучшего понимания, при построении карты стоит уделить внимание кластеризации, которая помогает сгруппировать переменные с похожими корреляциями, облегчая анализ.
Для более сложных случаев можно добавить аннотации и настроить цветовую палитру для выделения более важных участков карты. Выбор палитры и настройки визуализации зависят от целей анализа и предпочтений пользователя.
Как справиться с пропущенными данными при вычислении корреляции
При вычислении корреляции часто возникают проблемы с пропущенными значениями в наборе данных. Такие пропуски могут привести к искажению результатов, если не обработать их должным образом. Рассмотрим основные способы, как эффективно справиться с пропущенными данными при вычислении корреляции в Python.
- Удаление строк с пропущенными значениями: Один из простых методов – удалить все строки, содержащие хотя бы одно пропущенное значение. В Python для этого используется метод
dropna()библиотеки pandas.
import pandas as pd
df = df.dropna()Однако этот способ может не подойти, если пропусков слишком много, так как это может привести к потере значимой информации. Особенно важно быть осторожным при работе с малыми наборами данных.
- Заполнение пропущенных значений: Вместо удаления можно заменить пропуски на статистические значения, такие как среднее, медиана или мода. Важно учитывать, какой способ замены минимизирует искажения.
df.fillna(df.mean(), inplace=True)Если данные имеют временной характер, можно использовать метод заполнения пропусков на основе предыдущих или следующих значений, например, с помощью линейной интерполяции:
df.interpolate(method='linear', inplace=True)- Использование корреляции с пропусками (pairwise deletion): В некоторых случаях можно рассчитать корреляцию, игнорируя пропуски в отдельных парах значений. Это позволяет использовать максимально возможное количество данных без необходимости удаления целых строк или столбцов. В pandas это можно сделать, установив параметр
min_periodsв функцииcorr():
df.corr(min_periods=1)Однако этот подход может повлиять на точность корреляции, если пропусков слишком много в одной из переменных.
- Использование моделей для предсказания пропущенных значений: Для более сложных случаев можно применить модели машинного обучения для предсказания пропущенных значений, основываясь на других переменных. Методика наиболее эффективна, когда пропуски имеют структуру, зависящую от других признаков.
Пример использования модели линейной регрессии для предсказания пропусков:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# Подготовка данных
X = df.dropna(subset=['target_column'])
y = df['target_column'].dropna()
# Обучение модели
model = LinearRegression()
model.fit(X, y)
# Предсказание пропущенных значений
df['target_column'] = df['target_column'].fillna(model.predict(X))Этот подход позволяет сохранять информацию в данных, однако требует больше вычислительных ресурсов и более тщательной настройки модели.
- Применение методов для работы с недостающими данными в корреляции: Некоторые библиотеки, такие как
statsmodels, предлагают специальные методы для расчета корреляции, учитывающие пропуски в данных. Например, функцияpearsonr()изscipy.statsигнорирует пропущенные значения в расчетах.
from scipy.stats import pearsonr
corr, _ = pearsonr(df['column1'], df['column2'])Этот метод подходит, если пропуски случайны и не влияют на взаимосвязь между переменными.
В целом, выбор метода зависит от характеристик ваших данных и цели анализа. При наличии значительных пропусков важно учитывать потенциальное влияние каждого подхода на точность результатов корреляции.
Вопрос-ответ:
Что такое корреляция и зачем она нужна в анализе данных?
Корреляция – это мера того, как две переменные связаны между собой. В контексте анализа данных она помогает понять, насколько изменения одной переменной могут быть связаны с изменениями другой. Например, можно проверить, есть ли связь между количеством часов, которые студент тратит на учебу, и его оценками. Корреляция используется для выявления паттернов в данных и помогает в прогнозировании, принятии решений и выявлении возможных зависимостей.