
Проверка простоты числа является одной из базовых задач в программировании. В Python для этой цели существует несколько эффективных алгоритмов, которые могут быть реализованы как с использованием встроенных функций, так и с помощью написания собственных решений. Простое число – это такое число, которое больше 1 и делится только на 1 и на себя.
Самым прямым методом проверки простоты числа является перебор всех возможных делителей от 2 до квадратного корня числа. Если число делится на какой-либо из них, то оно не является простым. Эта оптимизация значимо снижает количество операций по сравнению с проверкой всех чисел до самого числа.
Пример реализации на Python выглядит следующим образом:
def is_prime(n):
if n <= 1:
return False
for i in range(2, int(n 0.5) + 1):
if n % i == 0:
return False
return TrueЭтот алгоритм проверяет, делится ли число на какой-либо из возможных делителей, начиная с 2 до квадратного корня числа. Использование квадратного корня как верхней границы для цикла – важная оптимизация, так как числа, большие корня числа, уже не могут быть делителями для чисел меньших данного значения.
Если вы хотите увеличить производительность программы для проверки простоты большого числа, можно использовать более сложные алгоритмы, такие как тесты Миллера-Рабина, который применяется для вероятностной проверки простоты числа. Этот метод позволяет проверять числа значительно быстрее, но с небольшой вероятностью ошибки, что подходит для работы с очень большими числами.
Как реализовать проверку простого числа с помощью цикла
Основная идея алгоритма заключается в том, что для проверки числа на простоту достаточно проверить делимость этого числа на числа от 2 до его квадратного корня. Если число делится на какое-либо из них, оно не является простым. Такой подход ускоряет выполнение программы, так как исключает проверку всех чисел до самого числа.
Рассмотрим пример реализации на Python:
def is_prime(n): if n <= 1: return False for i in range(2, int(n0.5) + 1): if n % i == 0: return False return True
В этом примере:
- Если число меньше или равно 1, оно сразу не является простым.
- Цикл начинается с 2 и проверяет делимость числа на все числа до квадратного корня из числа.
- Если число делится на какое-либо из этих чисел, оно не простое, и функция сразу возвращает
False. - Если цикл не находит делителей, возвращается
True, что означает, что число простое.
Этот способ достаточно эффективен для чисел средней величины. Для более крупных чисел можно использовать дополнительные оптимизации, такие как исключение четных чисел или использование алгоритмов с более сложной логикой (например, решето Эратосфена).
Использование оператора % для проверки на простоту

Для того чтобы проверить, является ли число простым, можно использовать цикл, который будет проверять делимость числа на все числа от 2 до его квадратного корня. Если остаток от деления (оператор %) равен 0 для любого из этих чисел, значит, число составное.
Пример кода для проверки числа на простоту с использованием оператора %:
def is_prime(n): if n <= 1: return False for i in range(2, int(n0.5) + 1): if n % i == 0: return False return True
В данном примере функция is_prime проверяет, делится ли число n на любое число от 2 до квадратного корня из n. Если делится, то число не простое, и функция возвращает False. В противном случае число считается простым, и функция возвращает True.
Использование оператора % в цикле позволяет эффективно и быстро определить, является ли число простым, минимизируя количество необходимых проверок.
Преимущества проверки числа с помощью метода «до квадратного корня»

Основные преимущества метода:
- Снижение сложности: Метод сокращает количество возможных делителей с N до примерно √N. Это значительно уменьшает время выполнения алгоритма для больших чисел.
- Оптимизация вычислений: Проверяя только до квадратного корня числа, можно значительно ускорить процесс, особенно для чисел порядка миллионов и миллиардов. Это достигается за счет уменьшения числа итераций.
- Легкость реализации: Алгоритм легко реализовать на Python с минимальными затратами памяти, так как не требуется хранить дополнительные данные или выполнять сложные операции.
- Экономия времени для больших чисел: В случае больших чисел, особенно при тестировании нескольких чисел подряд, метод до квадратного корня обеспечивает заметную экономию времени по сравнению с полным перебором всех делителей.
Пример реализации метода:
def is_prime(n): if n <= 1: return False for i in range(2, int(n0.5) + 1): if n % i == 0: return False return True
Применение данного метода особенно эффективно при тестировании чисел, в которых квадратный корень значительно меньше самого числа, например, в криптографических задачах или при нахождении простых чисел в пределах больших диапазонов.
Как избежать избыточных вычислений при проверке простоты
Если число не делится на числа до его квадратного корня, оно не имеет делителей, кроме единицы и самого себя. Например, для числа 29 достаточно проверить делители до 5 (поскольку √29 ≈ 5.39), что исключает необходимость проверки всех чисел до 29.
Дальнейшее улучшение заключается в учете четности чисел: достаточно проверять только делители, кратные 2 и 3, и избегать проверок для четных чисел, начиная с 4. Это сокращает количество операций вдвое.
Для улучшения можно использовать метод «проверки шагами». Например, после проверки числа на делимость на 2 и 3, можно проверять только числа вида 6k ± 1. Это еще больше сужает диапазон проверок и минимизирует вычисления.
Реализация: в Python оптимизированная проверка может выглядеть так:
def is_prime(n): if n <= 1: return False if n <= 3: return True if n % 2 == 0 or n % 3 == 0: return False i = 5 while i * i <= n: if n % i == 0 or n % (i + 2) == 0: return False i += 6 return True
Этот код проверяет простоту числа, начиная с делителей 2 и 3, а затем проверяет числа, кратные 6, с шагом 6. Такой подход значительно ускоряет проверку для больших чисел, сводя количество операций к минимуму.
Алгоритм проверки простоты с использованием функции
Вот пример такой функции:
def is_prime(n): if n <= 1: return False for i in range(2, int(n ** 0.5) + 1): if n % i == 0: return False return True
Функция is_prime(n) принимает число n и возвращает True, если число простое, и False в противном случае. Важно отметить, что алгоритм проверяет делимость только до квадратного корня числа, что значительно ускоряет процесс для больших чисел.
Основные моменты алгоритма:
- Если число меньше или равно 1, оно не может быть простым, поэтому сразу возвращается False.
- Цикл начинается с 2 и продолжается до квадратного корня числа. Если на каком-то шаге число делится на текущий делитель, оно не простое.
- Проверка до квадратного корня числа снижает количество операций. Например, для числа 100 достаточно проверить только делители от 2 до 10.
Этот метод является эффективным для чисел до 10 миллионов, но для очень больших чисел потребуется более сложные алгоритмы, такие как решето Эратосфена или другие методы с использованием теории чисел.
Проверка чисел на простоту с использованием библиотеки math
Для проверки числа на простоту можно эффективно использовать функции из стандартной библиотеки Python – math. Простой алгоритм для нахождения простоты числа подразумевает проверку, делится ли оно на какие-либо числа, кроме 1 и самого себя.
Основной метод для оптимизации проверки чисел заключается в том, чтобы проверять делимость только до квадратного корня из числа. Это позволяет значительно уменьшить количество операций, особенно для больших чисел.
Пример простого алгоритма с использованием библиотеки math:
import math def is_prime(n): if n <= 1: return False if n == 2 or n == 3: return True if n % 2 == 0 or n % 3 == 0: return False for i in range(5, int(math.sqrt(n)) + 1, 6): if n % i == 0 or n % (i + 2) == 0: return False return True
В этом примере функция is_prime() сначала исключает все четные числа и числа, делящиеся на 3, затем проверяет возможные делители от 5 до квадратного корня из числа с шагом 6. Это работает благодаря тому, что все числа, делящиеся на 2 или 3, уже были исключены.
Преимущества использования библиотеки math:
- Функция
math.sqrt()позволяет быстро вычислить квадратный корень числа, что сокращает количество проверок делимости. - Использование эффективного шага 6 позволяет исключить дополнительные операции с числами, которые точно не могут быть простыми (например, числа, делящиеся на 2 или 3).
Этот метод значительно быстрее, чем простое деление всех чисел подряд до самого числа, особенно когда речь идет о больших значениях.
Как ускорить проверку простого числа при больших значениях
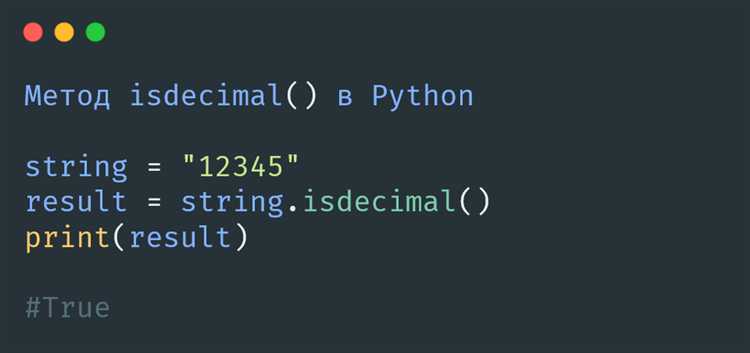
Кроме того, можно исключить четные числа, сразу после проверки числа на четность. Если число делится на 2, оно не является простым, и можно завершить проверку. После этого достаточно проверять только нечётные числа, начиная с 3.
Использование алгоритма "решето Эратосфена" может быть полезно при проверке сразу нескольких чисел на простоту. Он позволяет предварительно вычислить все простые числа до заданного предела. Для чисел, превышающих этот предел, можно использовать методы, такие как пробное деление до квадратного корня.
Также стоит учитывать оптимизации с использованием кеширования простых чисел или их хранения в списке. Если предполагается множество запросов на проверку чисел, этот подход может значительно ускорить процесс за счет быстрого поиска в уже вычисленных данных.
Другой способ ускорить проверку – это использование более сложных алгоритмов, например, теста Миллера-Рабина. Этот метод основан на вероятностных вычислениях и позволяет с высокой точностью проверять числа на простоту, особенно когда речь идет о больших числах, где стандартные алгоритмы работают медленно.
Вопрос-ответ:
Что такое простое число и как его проверить на Python?
Простое число — это натуральное число больше 1, которое не имеет делителей, кроме 1 и самого себя. Для проверки простоты числа на Python можно использовать цикл и проверку делимости. Например, можно пройтись по числам от 2 до квадратного корня числа и проверить, делится ли число на какое-либо из них. Если делится, то число не простое, если нет — оно простое.
Как оптимизировать проверку простого числа на Python?
Одним из способов оптимизации является сокращение диапазона для проверки делимости. Вместо проверки всех чисел до самого числа, можно проверить только до его квадратного корня. Также можно сразу исключить четные числа, проверяя только нечетные, что ускоряет процесс.
Почему в проверке простоты используется квадратный корень числа?
Квадратный корень числа — это точка, после которой все возможные делители числа повторяются в обратном порядке. Например, для числа 36, делители 2 и 18, 3 и 12, 4 и 9 — это пары, которые можно свести к одной проверке. Таким образом, достаточно проверять числа до квадратного корня, чтобы убедиться, что число не делится на другие числа.






