Алгоритм разложения числа на простые множители является важной задачей в различных областях, включая теорию чисел, криптографию и обработку данных. В Python существуют эффективные способы для выполнения этой задачи, которые позволяют быстро и с минимальными затратами ресурсов найти множители числа.
Один из основных методов заключается в использовании деления с остатком. Программа поочередно делит число на возможные простые числа, начиная с 2, и проверяет, делится ли оно на текущий кандидат. Как только деление на простое число дает остаток 0, это число становится простым множителем исходного числа. Этот процесс продолжается, пока остаток не станет равен 1 или не будут найдены все множители.
Пример на Python: для числа 56 разложение на простые множители выглядит так: 56 = 2 * 2 * 2 * 7. В Python можно реализовать такой алгоритм с помощью простого цикла. Стоит отметить, что время работы алгоритма сильно зависит от размера числа. Чем оно больше, тем больше шагов потребуется для его разложения.
Важно учитывать, что для больших чисел рекомендуется использовать более оптимизированные методы, такие как решето Эратосфена для поиска простых чисел, или более сложные алгоритмы, например, алгоритм пробного деления с отсечением по квадрату числа. Эти методы помогают значительно сократить время вычислений при работе с большими числами.
Подготовка среды для работы с разложением чисел в Python
Для разработки можно использовать любой удобный редактор кода, например, Visual Studio Code или PyCharm. Оба редактора поддерживают подсветку синтаксиса Python и позволяют удобно работать с проектами, содержащими несколько файлов. Также важно установить Python-расширения для выбранного редактора для повышения удобства работы.
Для работы с разложением чисел на простые множители не требуется никаких специфических внешних библиотек. Однако для улучшения производительности и расширения функционала можно использовать сторонние пакеты, такие как sympy, который предоставляет готовые функции для математических операций, включая разложение чисел на простые множители.
Для установки библиотеки sympy используйте команду:
pip install sympy
После установки библиотеки можно приступать к разложению чисел с помощью встроенных функций. Это будет полезно, если необходимо быстро и эффективно решать задачи без ручного написания алгоритмов разложения.
Если же вы хотите реализовать собственный алгоритм для разложения чисел, вам не потребуется дополнительных пакетов. Все необходимые функции можно написать с использованием стандартных возможностей Python, таких как циклы и условные операторы.
Для работы в командной строке Python используйте python -m venv для создания виртуальных окружений. Это поможет изолировать зависимости и избежать конфликтов между библиотеками разных проектов.
Кроме того, важно всегда тестировать и отлаживать ваш код. Для этого можно использовать встроенный модуль unittest, который позволяет легко создавать тесты и проверять корректность работы алгоритмов.
Использование алгоритма деления для нахождения простых множителей
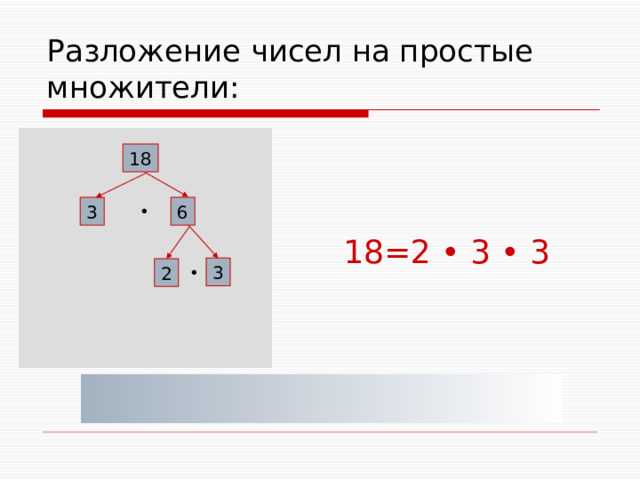
Алгоритм деления для нахождения простых множителей числа представляет собой процесс поочередного деления исходного числа на простые числа, начиная с наименьшего, пока результат деления не станет равным 1. Этот метод эффективен для разложения числа на множители, особенно когда требуется понять, из каких простых чисел состоит заданное число.
Для реализации алгоритма деления нужно начать с деления числа на 2, если оно чётное, и продолжать с каждым последующим простым числом (3, 5, 7 и т.д.), пока число не разделится на простые числа без остатка. Когда число делится без остатка, то найденный делитель добавляется в список простых множителей, а делённое число продолжает делиться на тот же делитель, пока это возможно. После этого процесс продолжается с следующим простым числом.
Алгоритм имеет одну особенность: если на каком-то этапе число становится меньше делителя, то дальнейшее деление по этим правилам невозможно, и оставшееся число либо является простым, либо 1. В случае, если на последнем этапе осталось простое число, оно также добавляется в список множителей.
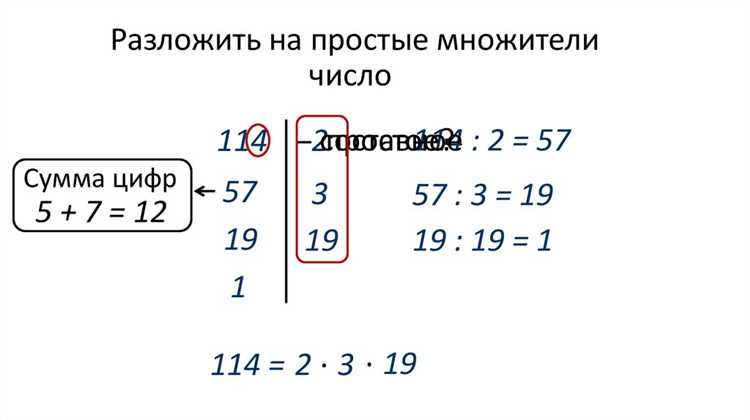
Пример работы алгоритма: разложим число 60. Начнём с 2, поскольку 60 чётное, делим на 2 – получаем 30. Далее снова делим на 2 – 30 делится на 2, результат 15. Число 15 не делится на 2, пробуем 3. 15 делится на 3, результат 5. Теперь 5 – простое число, и процесс завершён. Множители числа 60: 2, 2, 3, 5.
Этот метод идеально подходит для чисел относительно небольших значений. При разложении больших чисел на множители использование более сложных алгоритмов, например, тестов на простоту или решета Эратосфена, может быть более эффективным.
Как написать функцию для разложения числа на простые множители

Для разложения числа на простые множители в Python достаточно воспользоваться простым алгоритмом. Основная идея заключается в том, чтобы поочередно делить число на простые числа, начиная с 2, и продолжать до тех пор, пока число не станет равным 1.
Основной принцип заключается в том, что любое составное число можно выразить через простые множители. Например, для числа 60 разложение будет таким: 60 = 2 × 2 × 3 × 5. Для этого мы будем использовать цикл, который будет проверять делимость числа на текущий возможный множитель, начиная с 2. Как только число делится на текущий множитель, его нужно разделить, и повторить операцию, пока делимость сохраняется.
Пример реализации функции:
def prime_factors(n): factors = [] divisor = 2 while n >= divisor: if n % divisor == 0: factors.append(divisor) n //= divisor else: divisor += 1 return factors
Функция принимает целое число n и возвращает список его простых множителей. Внутри функции используется цикл, который пробует разделить число на 2, затем на 3, и так далее. Когда число делится на текущий делитель, он добавляется в список, а само число делится на этот делитель.
Важный момент: когда число больше или равно делителю, нужно проверять его делимость. Если число не делится на текущий делитель, увеличиваем делитель на 1 и пробуем снова. Этот алгоритм эффективен для большинства задач по разложению на простые множители.
Функция работает корректно для всех чисел, включая простые, которые не будут разложены на меньшие множители (например, 7 останется 7). Для оптимизации алгоритма можно остановить цикл, когда текущий делитель превышает квадратный корень из числа. Это уменьшит количество проверок и ускорит выполнение.
В итоге, для числа 60 пример вызова функции будет выглядеть так:
Пример разложения числа на простые множители с использованием библиотеки SymPy
Для разложения числа на простые множители в Python можно использовать библиотеку SymPy, которая предоставляет удобные инструменты для работы с числами и математическими выражениями. В частности, для этой задачи используется функция factorint().
Пример разложения числа 56 на простые множители:
from sympy import factorint number = 56 factors = factorint(number) print(factors)
После выполнения этого кода на экран будет выведен словарь, в котором ключами являются простые множители, а значениями – их степени. Для числа 56 результат будет таким:
{2: 3, 7: 1}
Это означает, что 56 разлагается как 2³ * 7.
Библиотека SymPy также позволяет работать с большими числами, обеспечивая точность разложения. Важно отметить, что для разложения чисел, превышающих 10⁶, SymPy применяет более сложные алгоритмы, что значительно ускоряет процесс.
Использование factorint() является простым и эффективным способом получения простых множителей числа с минимальными затратами времени и ресурсов.
Обработка больших чисел при разложении на простые множители
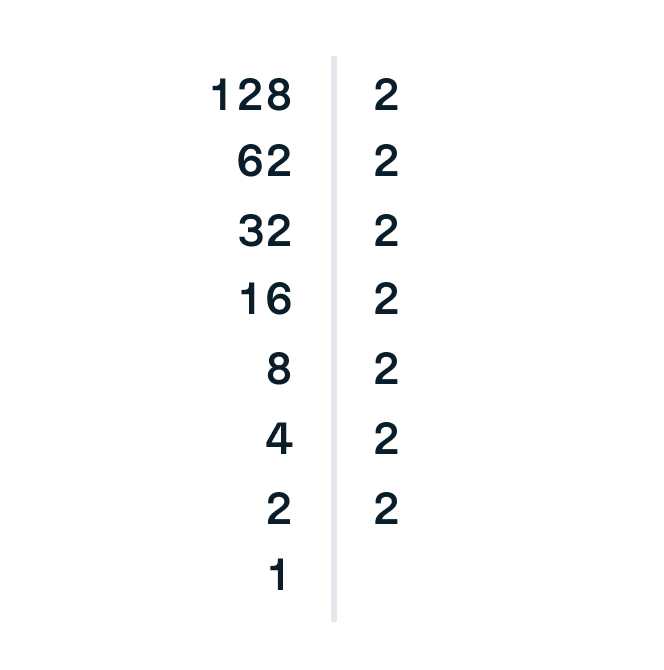
Разложение на простые множители больших чисел – сложная задача, требующая оптимизированных алгоритмов. Проблема заключается в том, что простое разложение требует проверки множества возможных делителей, что может быть крайне ресурсоемким процессом для чисел с большим количеством цифр.
Основной подход к разложению больших чисел – это использование эффективных методов тестирования делимости и алгоритмов факторизации, таких как метод пробного деления, решето Эратосфена, алгоритм Миллера-Рабина и алгоритм Ленстры. Разберем их особенности на примере Python.
Для чисел размером в 20 и более цифр стандартный метод пробного деления становится слишком медленным, так как потребует многократных проверок делимости для чисел, которые растут экспоненциально. Использование метода пробного деления эффективно для чисел до 10^9. Для более крупных чисел предпочтительно использовать более сложные алгоритмы, такие как метод квадратичного решета, решето Полларда и алгоритм Карриса. Например, при разложении числа в 50 цифр, например, с использованием алгоритма Карриса, время разложения может значительно сократиться по сравнению с методом пробного деления.
В Python для обработки больших чисел можно использовать встроенные библиотеки, такие как `sympy`, которая предоставляет функции для быстрого разложения чисел на множители. Пример использования:
from sympy import factorint number = 123456789012345 factors = factorint(number) print(factors)
Этот код разложит число на простые множители, используя оптимизированные алгоритмы. Однако, для чисел порядка 10^15 и более важно учитывать не только время работы, но и потребление памяти.
Для более крупных чисел важно помнить о памяти, так как большие числа требуют значительных объемов памяти для хранения промежуточных результатов. Например, при разложении числа порядка 10^50 может потребоваться несколько гигабайт оперативной памяти. Использование распределенных вычислений может быть полезным для ускорения процесса разложения на простые множители при обработке чрезвычайно больших чисел.
Кроме того, для оптимизации работы с большими числами можно использовать метод параллельных вычислений, разбивая задачу на несколько частей и используя многозадачность. Это позволяет ускорить процесс разложения на простые множители и снизить нагрузку на процессор.
Оптимизация алгоритмов для ускорения разложения больших чисел

Для разложения больших чисел на простые множители важна не только корректность алгоритма, но и его эффективность. Простое деление с проверкой на простоту может оказаться слишком медленным для больших чисел, поэтому требуется использовать более продвинутые методы оптимизации.
- Использование метода Эратосфена для поиска простых чисел – Прежде чем начинать разложение числа, можно сгенерировать список простых чисел до определённого предела с помощью решета Эратосфена. Это позволяет быстро находить возможные делители, исключив проверки всех чисел подряд.
- Оптимизация проверки делимости – Вместо того чтобы проверять делимость на все числа подряд, ограничьте проверку квадратным корнем из числа. Если число делится на какое-либо простое число, то один из множителей обязательно будет меньше или равен корню из исходного числа.
- Использование метода пробного деления с шагом через 2 – Если число чётное, можно сразу разделить его на 2. Далее для нечётных чисел проверку делимости имеет смысл начинать с 3 и увеличивать шаг на 2 (проверяя только нечётные числа). Это значительно ускоряет процесс по сравнению с проверкой всех чисел подряд.
- Алгоритм Миллера-Рабина для проверки простоты чисел – Когда проверка делимости стандартными методами становится слишком затратной, можно использовать вероятностный тест Миллера-Рабина для проверки простоты больших чисел. Это позволяет исключить числа, которые с большой вероятностью не являются простыми.
- Метод Кармайкла для ускоренной факторизации – Алгоритм Кармайкла помогает разделить число на множители, избегая чрезмерных проверок. Это особенно эффективно для чисел, у которых большие простые множители.
- Использование квадратичного решета – Квадратичное решето эффективно работает для чисел с несколькими большими простыми множителями, ускоряя нахождение факторов через использование квадратичных форм.
Комбинируя эти методы, можно значительно ускорить разложение больших чисел, минимизируя затраты по времени на каждую операцию. Одним из самых эффективных решений для масштабируемой факторизации является использование сочетания пробного деления с продвинутыми методами, такими как метод Кармайкла или квадратичное решето. Важно подобрать оптимальную стратегию в зависимости от размера числа и требуемой точности вычислений.
Вопрос-ответ:
Почему при разложении числа на простые множители я использую цикл до квадратного корня из числа?
Когда мы ищем простые множители числа, проверка делителей до квадратного корня числа достаточно эффективна. Это объясняется тем, что если число n делится на какое-либо число большее, чем его квадратный корень, то соответствующий делитель будет уже найден в предыдущих проверках. Например, если n делится на число больше квадратного корня, то второй множитель обязательно будет меньше квадратного корня. Таким образом, проверка делителей до квадратного корня уменьшает количество операций.