Как работает градиентный бустинг python numpy

Градиентный бустинг – это мощная техника машинного обучения, широко используемая для решения задач регрессии и классификации. Алгоритм строит модель путем поэтапного улучшения ошибок, совершенных предыдущими моделями, используя принцип наибольшего уменьшения ошибки на каждом шаге. В этом процессе каждое новое дерево корректирует прогнозы предыдущих, что позволяет достичь высокой точности. В Python эта техника реализуется с использованием популярных библиотек, таких как Numpy для числовых вычислений и фреймворков, например, Scikit-learn.

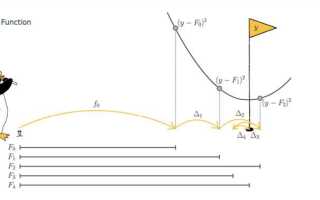
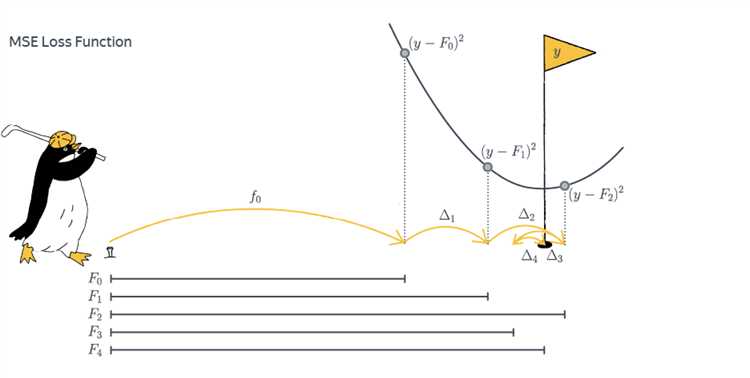
Основной принцип градиентного бустинга заключается в минимизации функции потерь с помощью итеративного обучения. На каждом шаге алгоритм строит новое дерево решений, которое направлено на уменьшение остаточной ошибки. Важно отметить, что на каждом этапе обучения алгоритм использует градиент функции потерь, чтобы определить направление и шаг, на который нужно двигаться, чтобы минимизировать ошибку. Таким образом, каждое следующее дерево направлено на исправление ошибок предыдущих.

Пример работы алгоритма: на первом шаге строится простое дерево, которое предсказывает значение для каждого объекта. После этого вычисляется остаточная ошибка (разница между реальными и предсказанными значениями). На следующем шаге строится новое дерево, которое обучается на этих ошибках, а процесс повторяется, пока не достигнуты заданные критерии остановки, такие как максимальное количество деревьев или минимальное улучшение ошибки.

Для реализации градиентного бустинга с использованием Python и Numpy важно понимать основные компоненты алгоритма. Во-первых, необходимо правильно настроить функцию потерь, которая будет оптимизироваться в процессе обучения. Во-вторых, стоит учесть, что градиентный бустинг требует аккуратной настройки гиперпараметров, таких как скорость обучения, количество деревьев и глубина дерева, так как эти параметры сильно влияют на производительность модели.

Использование Numpy в этом процессе позволяет эффективно работать с массивами данных и вычислять необходимые значения, такие как градиенты функции потерь. В отличие от более высокоуровневых библиотек, Numpy дает более глубокий контроль над каждым шагом алгоритма, что может быть полезно для экспериментов и оптимизации.

Предобработка данных для градиентного бустинга с использованием Numpy

Первый шаг – это обработка пропущенных значений. В зависимости от ситуации, пропуски можно заполнять средним, медианой или использовать более сложные методы импутации. Для числовых признаков с использованием Numpy можно легко заменить пропущенные значения на среднее:

import numpy as np
data = np.array([1, 2, np.nan, 4, 5])
mean_value = np.nanmean(data)
data[np.isnan(data)] = mean_value

Для категориальных признаков пропущенные значения можно заполнить наиболее часто встречающимся значением, используя функцию np.nan и np.bincount, если это необходимо.

После обработки пропусков следует нормализация или стандартизация данных. Градиентный бустинг не требует жесткой нормализации, но стандартизация может ускорить сходимость алгоритма. Для этого можно использовать стандартное отклонение и среднее значение:

mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
data_standardized = (data - mean) / std

Если данные содержат категориальные признаки, их необходимо кодировать. Простой подход – это использование one-hot кодирования, где для каждого уникального значения создается отдельный бинарный столбец. В Numpy это можно сделать следующим образом:

categories = np.array([1, 2, 1, 3, 2])
one_hot = np.eye(np.max(categories) + 1)[categories - 1]

После преобразования категориальных признаков можно выполнить разделение данных на тренировочные и тестовые выборки. Для этого удобно использовать случайную подрезку:

indices = np.random.permutation(len(data))
train_size = int(0.8 * len(data))
train_data = data[indices[:train_size]]
test_data = data[indices[train_size:]]

Наконец, важно убедиться, что все признаки имеют одинаковую масштабируемость, чтобы избежать ситуации, когда один признак доминирует в процессе обучения из-за большей амплитуды значений. В случае работы с числовыми данными рекомендуется привести все признаки к одному масштабу, используя минимаксную нормализацию:

data_min = np.min(data, axis=0)
data_max = np.max(data, axis=0)
data_scaled = (data - data_min) / (data_max - data_min)

Эти шаги являются основой предобработки данных перед применением градиентного бустинга с использованием Numpy. Правильная подготовка данных снижает вероятность ошибок в модели и повышает её точность.

Реализация базового алгоритма градиентного бустинга на Python и Numpy

Для начала создадим простую реализацию алгоритма градиентного бустинга с использованием минимальных зависимостей. В этой реализации предполагается, что основная цель – предсказать выходные значения на основе входных данных, используя деревья решений и корректируя ошибку каждой новой моделью.

1. Инициализация модели: Начнём с создания базовой модели. На первом шаге алгоритм обучается на среднем значении целевой переменной. Это значение служит для вычисления ошибок на следующих шагах.

2. Обучение слабых моделей: На каждом следующем шаге алгоритм находит ошибку предыдущей модели и строит новое дерево, которое минимизирует эту ошибку. В процессе используется метод градиентного спуска для оптимизации параметров деревьев.

3. Обновление модели: После каждой итерации обновляется результат предсказания, добавляя предсказания нового дерева с небольшим коэффициентом (learning rate), чтобы избежать переобучения. Алгоритм повторяет этот процесс до тех пор, пока не будет достигнут заранее заданный порог ошибок или количество итераций.

Пример кода для реализации базового градиентного бустинга:

import numpy as np
# Функция для вычисления градиента (ошибки)
def compute_gradient(y_true, y_pred):
return y_true - y_pred
# Функция для обновления предсказаний
def update_predictions(predictions, gradient, learning_rate=0.1):
return predictions + learning_rate * gradient
# Реализация градиентного бустинга
def gradient_boosting(X, y, n_estimators=100, learning_rate=0.1):
n_samples, n_features = X.shape
predictions = np.full_like(y, np.mean(y), dtype=np.float32)  # Начальное предсказание - среднее значение
for estimator in range(n_estimators):
# Вычисляем ошибку (градиент)
gradient = compute_gradient(y, predictions)
# Обновляем предсказания
predictions = update_predictions(predictions, gradient, learning_rate)
return predictions
# Пример использования
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])  # Пример входных данных
y = np.array([1, 2, 3, 4])  # Пример целевых значений
predictions = gradient_boosting(X, y)
print(predictions)

Этот код представляет собой минимальную версию градиентного бустинга, которая использует простое обновление на основе градиента для корректировки ошибок предсказаний. Основное внимание в реализации уделяется корректировке предсказаний в каждом цикле с использованием градиента.

Основной момент, на который стоит обратить внимание, – это коэффициент обучения (learning rate), который контролирует скорость обновления модели. Слишком большой learning rate может привести к переобучению, а слишком маленький – к слишком медленному обучению.

В реальной задаче обычно используются более сложные структуры, такие как деревья решений с ограниченной глубиной, чтобы ускорить обучение и повысить точность. Тем не менее, эта простая реализация даёт хорошее понимание принципа работы градиентного бустинга и позволяет модифицировать его для более сложных задач.

Оптимизация гиперпараметров в модели градиентного бустинга с Numpy

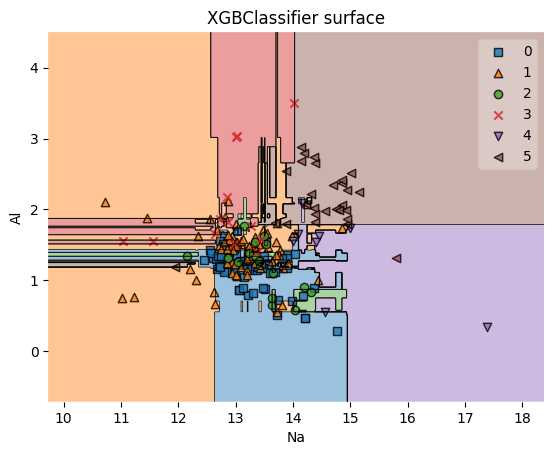
Оптимизация гиперпараметров в модели градиентного бустинга важна для повышения точности прогноза. При использовании Numpy для реализации градиентного бустинга важно настроить параметры, такие как количество деревьев, скорость обучения, максимальная глубина деревьев и минимальное количество примеров в листьях, чтобы добиться наилучших результатов.

Для начала, необходимо определить ключевые гиперпараметры, которые влияют на обучение модели:

• Количество деревьев (n_estimators): Чем больше деревьев, тем более точной будет модель, но при этом увеличится время обучения и вероятность переобучения. Обычно начинают с 100-200 деревьев.
• Скорость обучения (learning_rate): Чем ниже скорость обучения, тем медленнее модель будет сходиться. Однако меньшая скорость обучения требует большего числа деревьев для достижения хорошего результата. Рекомендуемые значения: от 0.01 до 0.1.
• Максимальная глубина деревьев (max_depth): Определяет глубину каждого дерева. Ограничение глубины помогает предотвратить переобучение. Хорошие начальные значения: от 3 до 6.
• Минимальное количество примеров в листьях (min_samples_leaf): Этот параметр контролирует минимальное количество данных, которые должны быть в листьях дерева. Обычно значение 1-10 подходит для большинства задач.

Оптимизация гиперпараметров может быть выполнена с помощью различных методов. Один из них – использование сеточного поиска (Grid Search). В этом методе создаются разные комбинации гиперпараметров, и для каждой из них обучается модель. Это позволяет выбрать наилучшие параметры, но при этом может быть вычислительно затратным.

Для более эффективной оптимизации можно использовать случайный поиск (Random Search). В отличие от сеточного поиска, случайный поиск выбирает случайные комбинации гиперпараметров, что позволяет быстрее найти хорошие результаты при меньших вычислительных затратах.

Пример кода для настройки гиперпараметров с использованием случайного поиска:

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import RandomizedSearchCV
# Параметры для случайного поиска
param_dist = {
'n_estimators': [50, 100, 150, 200],
'learning_rate': [0.01, 0.1, 0.05],
'max_depth': [3, 4, 5, 6],
'min_samples_leaf': [1, 2, 5]
}
# Инициализация модели
model = GradientBoostingClassifier()
# Инициализация случайного поиска
random_search = RandomizedSearchCV(model, param_distributions=param_dist, n_iter=100, cv=3, random_state=42)
# Обучение модели
random_search.fit(X_train, y_train)
# Лучшие параметры
best_params = random_search.best_params_

Для того чтобы избежать переобучения, также полезно использовать кросс-валидацию. Это позволяет проверять модель на разных частях данных и минимизировать влияние случайных факторов.

Другим эффективным методом оптимизации является использование байесовской оптимизации. Этот метод основывается на построении вероятностной модели, которая предсказывает, какие гиперпараметры будут наиболее эффективными. Для его реализации можно использовать библиотеку scikit-optimize или hyperopt.

Важно помнить, что оптимизация гиперпараметров – это итеративный процесс, требующий значительных вычислительных ресурсов, особенно при большом количестве параметров и данных. Рекомендуется начинать с грубых параметров, а затем сужать диапазоны в процессе экспериментов.

Как уменьшить переобучение в градиентном бустинге с помощью регуляризации

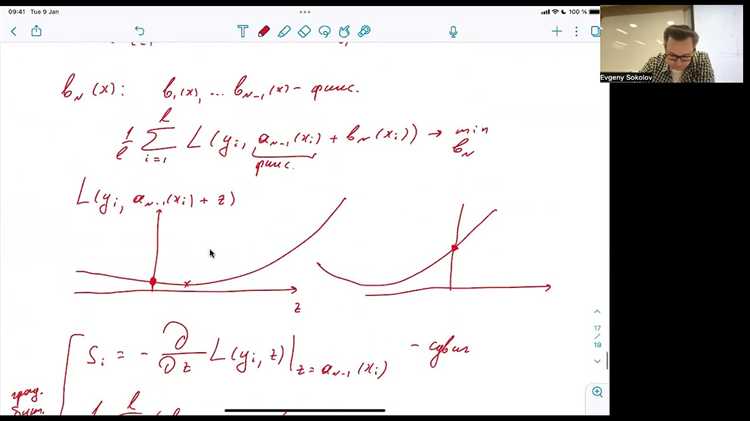
Основные подходы к регуляризации в градиентном бустинге:

1. Ограничение глубины деревьев

Глубина деревьев напрямую влияет на сложность модели. Чем глубже дерево, тем больше его способность подгонять данные, что ведет к переобучению. Чтобы уменьшить этот эффект, устанавливают максимальную глубину деревьев с помощью параметра max_depth. Часто достаточно ограничить глубину деревьев значением 3–5 для предотвращения чрезмерного подгона.

2. Использование минимального числа образцов для разбиения узла

Регуляризация также может быть достигнута путем ограничения минимального числа образцов, которые должны быть в узле для его разделения. Этот параметр называется min_samples_split. Увеличение значения этого параметра препятствует созданию слишком сложных деревьев, которые могут переобучаться.

3. Количество деревьев и скорость обучения

Для предотвращения переобучения важен правильный баланс между количеством деревьев и скоростью обучения. Слишком большое количество деревьев может привести к переобучению, особенно если модель учится слишком быстро. Использование параметра learning_rate (скорость обучения) позволяет контролировать шаг, с которым модель обновляет веса. Низкая скорость обучения (learning_rate < 0.1) в сочетании с увеличением числа деревьев помогает модели находить более стабильные и обоснованные зависимости, но это требует большего времени для обучения.

4. Регуляризация с помощью ранней остановки

Ранняя остановка помогает избежать переобучения, прекращая обучение, когда на валидационных данных не наблюдается улучшений. Это достигается путем отслеживания ошибки на валидационном наборе данных и прекращения обучения, если ошибка не снижается после определенного числа итераций. В XGBoost для этого можно использовать параметр early_stopping_rounds.

5. Случайный лес деревьев и подвыборка

В градиентном бустинге можно использовать подвыборку данных и случайный выбор признаков для каждого дерева, что уменьшает зависимость от конкретных данных. Параметр subsample управляет количеством данных, используемых для обучения каждого дерева. Если установить subsample в 0.8, то каждый элемент будет использовать только 80% данных для обучения, что может снизить переобучение.

6. Линейная регуляризация

Некоторые реализации градиентного бустинга поддерживают линейную регуляризацию через параметр lambda, который помогает уменьшить веса, сильно влияющие на решение модели. Это дополнительный способ борьбы с переобучением, который используется в сочетании с другими методами регуляризации.

Применение этих методов позволяет снизить переобучение в градиентном бустинге, улучшая стабильность модели и её способность к обобщению.

Оценка производительности модели градиентного бустинга с использованием метрик на Python

Для оценки качества модели градиентного бустинга обычно применяются различные метрики, в зависимости от задачи (регрессия или классификация). Рассмотрим, как правильно использовать эти метрики с помощью Python и Numpy.

В задачах регрессии наиболее популярными метриками являются среднеквадратичная ошибка (MSE), средняя абсолютная ошибка (MAE) и коэффициент детерминации (R2). Для расчета MSE и MAE достаточно вычислить разницу между предсказанными и реальными значениями, а затем агрегировать её. Например, для MSE можно использовать следующий код:

import numpy as np
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])
mse = np.mean((y_true - y_pred)2)
print(f'MSE: {mse}')

mae = np.mean(np.abs(y_true - y_pred))
print(f'MAE: {mae}')

ss_total = np.sum((y_true - np.mean(y_true))2)
ss_residual = np.sum((y_true - y_pred)**2)
r2 = 1 - (ss_residual / ss_total)
print(f'R2: {r2}')

Для задач классификации используются другие метрики. Точность (accuracy), precision, recall и F1-меры дают более полное представление о производительности модели. Пример расчета точности:

from sklearn.metrics import accuracy_score
y_true = np.array([0, 1, 1, 0, 1])
y_pred = np.array([0, 0, 1, 0, 1])
accuracy = accuracy_score(y_true, y_pred)
print(f'Accuracy: {accuracy}')

Чтобы получить precision, recall и F1-меру, используйте встроенные функции из sklearn.metrics:

from sklearn.metrics import precision_score, recall_score, f1_score
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
print(f'Precision: {precision}, Recall: {recall}, F1: {f1}')

Для оценки модели в процессе обучения полезно использовать кривые обучения и валидации. Для этого можно строить графики, показывающие изменение ошибок по мере увеличения количества деревьев в модели. Это помогает выбрать оптимальное количество итераций для градиентного бустинга, избегая переобучения.

Чтобы избежать переобучения, стоит также обратить внимание на метрики AUC-ROC и площадь под кривой для классификационных задач. Чем выше значение AUC, тем лучше модель различает классы. Для расчета AUC:

from sklearn.metrics import roc_auc_score
roc_auc = roc_auc_score(y_true, y_pred)
print(f'AUC: {roc_auc}')

Также не забудьте о кросс-валидации, чтобы получить более стабильные и точные оценки. В sklearn для этого существует функция cross_val_score, которая позволяет автоматически разделить данные на обучающие и тестовые наборы и оценить модель на разных фолдах.

Вопрос-ответ:

Что такое градиентный бустинг и как он работает на Python с использованием Numpy?

Градиентный бустинг — это метод ансамблирования, который использует несколько моделей для улучшения предсказаний. Суть его работы заключается в том, что каждая последующая модель обучается на ошибках предыдущей. В Python можно реализовать градиентный бустинг с помощью библиотеки Numpy, создавая слабые модели, такие как решающие деревья, и постепенно исправляя ошибки этих моделей. Для этого на каждом шаге вычисляются градиенты ошибки и обучается новая модель, минимизирующая эту ошибку.

Какие математические основы лежат в основе градиентного бустинга?

Основной математический принцип градиентного бустинга — это использование градиента функции потерь для поиска оптимальной модели. На каждом шаге строится модель, которая минимизирует ошибку предыдущей модели, используя градиент этого шага. Алгоритм подходит для задачи регрессии и классификации. Если говорить о конкретных вычислениях, на каждом шаге вычисляется градиент функции потерь по отношению к предсказаниям текущей модели, что позволяет корректировать модель, минимизируя ошибку.

Почему градиентный бустинг так популярен в машинном обучении?

Градиентный бустинг популярен благодаря своей способности показывать отличные результаты при работе с различными типами данных. Он позволяет создавать мощные модели, даже если используется большое количество простых слабых моделей. Важная особенность этого метода — это способность адаптироваться к данным, улучшая точность на каждом шаге обучения. Реализация градиентного бустинга на Python с использованием Numpy дает гибкость и контроль над процессом обучения, что делает его удобным инструментом для разработчиков.

Как можно реализовать градиентный бустинг на Python с помощью Numpy? Есть ли примеры кода?

Для реализации градиентного бустинга на Python с использованием Numpy, необходимо вручную реализовать алгоритм обучения, шаг за шагом обучая модель на ошибках предыдущей. Пример кода может включать использование решения деревьев, например, с помощью библиотеки Numpy для математических операций. Примерная схема кода: на каждом шаге вычисляется ошибка, которая затем используется для обучения следующей модели. Код будет выглядеть как последовательность операций, где на каждом этапе происходит корректировка предсказания.

Как градиентный бустинг отличается от других методов ансамблирования, например, от случайного леса?

Основное отличие между градиентным бустингом и случайным лесом заключается в способе формирования ансамбля моделей. В случае случайного леса все деревья строятся параллельно и независимы друг от друга, тогда как в градиентном бустинге каждое новое дерево строится последовательно, пытаясь минимизировать ошибки предыдущих деревьев. Таким образом, градиентный бустинг может достичь более высокой точности за счет корректировки ошибок на каждом шаге, в то время как случайный лес является более стабильным и менее чувствительным к ошибкам.