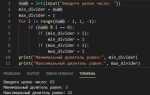
Сдвиг элементов массива вправо – операция, при которой каждый элемент перемещается на одну или несколько позиций вперёд, а последние значения переходят в начало структуры. В Python это часто требуется при решении задач на циклические перестановки, реализацию кольцевых буферов и в алгоритмах шифрования.
Стандартные средства языка позволяют реализовать сдвиг без использования внешних библиотек. Например, список lst = [1, 2, 3, 4] после сдвига на одну позицию вправо становится [4, 1, 2, 3]. Это достигается выражением lst[-1:] + lst[:-1]. Такой подход работает за O(n) по времени и требует O(n) дополнительной памяти.
Для сдвига на k позиций используется формула k %= len(lst), чтобы избежать избыточных итераций. Затем выполняется операция lst[-k:] + lst[:-k]. Такой метод универсален и подходит для списков любой длины и типа содержимого.
Если критична производительность и нежелательно создание нового списка, предпочтительнее использовать модуль collections и объект deque. Метод deque.rotate(k) выполняет сдвиг на месте за O(k), что особенно полезно при работе с большими объемами данных.
Выбор метода зависит от конкретной задачи: требуется ли сохранить оригинальный массив, важна ли скорость или минимизация памяти. Python предоставляет достаточную гибкость для реализации всех вариантов.
Как сдвинуть список вправо на один элемент с сохранением порядка
Для смещения всех элементов списка на одну позицию вправо с сохранением их последовательности достаточно воспользоваться срезами. Рассмотрим пример:
lst = [10, 20, 30, 40]
lst = [lst[-1]] + lst[:-1]
Результат: [40, 10, 20, 30]. Последний элемент lst[-1] перемещается в начало, а остальные элементы сдвигаются на одну позицию вправо за счёт lst[:-1].
Альтернативный способ с использованием метода insert:
lst = [10, 20, 30, 40]
lst.insert(0, lst.pop())
Функция pop() удаляет и возвращает последний элемент, а insert(0, ...) вставляет его в начало. Итог – тот же: [40, 10, 20, 30].
Оба способа работают за время O(n), не создают дополнительных списков (кроме первого, где создаётся новый список), и подходят для небольших и средних по размеру последовательностей. Для длинных списков предпочтительнее второй вариант, так как он не требует выделения памяти под копию.
Сдвиг вправо на N позиций с использованием срезов

Срезы позволяют выполнить сдвиг массива без циклов и сторонних библиотек. Для массива arr и значения сдвига n используется выражение arr[-n:] + arr[:-n]. Оно формирует новый массив, где последние n элементов перемещаются в начало, а остальные – следуют за ними.
Пример: при arr = [1, 2, 3, 4, 5] и n = 2 результатом будет [4, 5, 1, 2, 3].
Для избежания выхода за пределы массива при n > len(arr) следует использовать n = n % len(arr). Это гарантирует корректный сдвиг независимо от значения n.
Срезы не изменяют исходный массив. Чтобы обновить его, можно присвоить результат обратно: arr = arr[-n:] + arr[:-n].
При работе со списками большой длины срезы обеспечивают высокую производительность за счёт обращения к памяти без явных итераций. Однако для массивов с миллионами элементов стоит учитывать накладные расходы на создание нового списка.
Использование collections.deque для циклического сдвига

Модуль collections предоставляет структуру deque, оптимизированную для быстрого добавления и удаления элементов с обоих концов. Для циклического сдвига элементов массива вправо deque обладает встроенным методом rotate(), работающим за время O(k), где k – величина сдвига.
- Импорт:
from collections import deque - Создание очереди:
dq = deque([1, 2, 3, 4, 5]) - Сдвиг вправо на 2 позиции:
dq.rotate(2) - Результат:
deque([4, 5, 1, 2, 3])
Преимущества:
- Сдвиг без создания копий: изменение выполняется на месте
- Поддержка отрицательного сдвига:
dq.rotate(-k)– сдвиг влево - Подходит для массивов с большим числом элементов благодаря эффективности операций на концах
Рекомендации:
- Преобразовывайте список в
dequeтолько при необходимости многократных сдвигов - Для однократного сдвига предпочтительнее срезы списков: они быстрее при небольших объёмах данных
- Не используйте
dequeдля произвольного доступа по индексу – это медленнее, чем у обычного списка
Обработка сдвига, превышающего длину списка

При сдвиге элементов вправо на количество позиций, превышающее длину списка, возникает избыточное количество циклов, не влияющих на результат. Это ведет к ненужным вычислениям. Чтобы избежать этого, необходимо привести значение сдвига к диапазону от 0 до len(lst) - 1 с помощью операции взятия остатка от деления.
Пример:
lst = [1, 2, 3, 4, 5]
shift = 12
n = len(lst)
k = shift % n
shifted = lst[-k:] + lst[:-k]
print(shifted)Результат:
[4, 5, 1, 2, 3]Значение k принимает значение 2, поскольку 12 % 5 = 2. Это обеспечивает корректную перестановку элементов без лишних итераций и не требует дополнительных проверок в логике.
Если список пустой, деление на длину вызовет исключение ZeroDivisionError. Поэтому перед вычислением сдвига следует добавить проверку:
if lst:
k = shift % len(lst)
shifted = lst[-k:] + lst[:-k]
else:
shifted = []Эта практика особенно важна при работе с большими массивами или при использовании значения сдвига, полученного из внешнего источника. Приведение сдвига к модулю длины позволяет избежать ошибок и сохраняет производительность.
Сдвиг вложенных списков вправо по строкам
Для сдвига элементов во вложенных списках (двумерных массивах) вправо по строкам требуется обработка каждой подстроки отдельно. Предположим, есть список вида:
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]Чтобы сдвинуть каждый ряд на один элемент вправо, используется операция среза:
for i in range(len(matrix)):
matrix[i] = [matrix[i][-1]] + matrix[i][:-1]Результат:
[
[3, 1, 2],
[6, 4, 5],
[9, 7, 8]
]Ключевые аспекты:
1. Изменения не влияют на другие строки: обработка идет построчно, без вмешательства в остальные уровни вложенности.
2. Сложность операции линейна: каждая строка обрабатывается за O(n), где n – длина строки.
3. Сдвиг на произвольное количество шагов: чтобы сдвиг был на k позиций:
k = 2
for i in range(len(matrix)):
matrix[i] = matrix[i][-k:] + matrix[i][:-k]Важно следить за тем, чтобы k ≤ len(matrix[i]) для каждой строки, иначе стоит использовать k = k % len(matrix[i]).
Такая техника актуальна при работе с табличными структурами, где требуется циклическое смещение данных.
Изменение списка на месте без создания нового объекта
Основной подход к изменению списка на месте заключается в использовании срезов и встроенных методов списка. В случае сдвига элементов вправо, можно использовать срезы, чтобы переместить элементы без создания дополнительных объектов.
Пример сдвига элементов вправо на одно место:
list = [1, 2, 3, 4, 5] list[:0] = [list.pop()] print(list) # [5, 1, 2, 3, 4]
В данном примере используется метод pop(), чтобы удалить последний элемент, а затем срез списка list[:0] вставляет его в начало. Это изменение происходит на месте, и исходный объект списка не изменяется.
Для более сложных сдвигов (например, сдвиг на несколько позиций) можно комбинировать срезы с циклическим сдвигом:
def shift_right(lst, n): n = n % len(lst) # Обеспечивает корректность для n, превышающего длину списка lst[:0] = lst[-n:] lst[-n:] = [] lst = [1, 2, 3, 4, 5] shift_right(lst, 2) print(lst) # [4, 5, 1, 2, 3]
Здесь функция shift_right сдвигает список на несколько позиций вправо. Сначала извлекаются последние n элементов, затем они вставляются в начало списка, а оставшиеся элементы удаляются с конца.
Важно помнить, что изменение на месте изменяет сам объект, поэтому при передаче списка в функцию мы работаем с оригинальным объектом, а не с его копией. Это полезно, когда нужно обновить данные без использования лишней памяти.
Использование таких методов, как срезы и методы работы со списками, позволяет эффективно изменять данные без лишних затрат на создание новых объектов. Это подходит для задач, где необходимо оптимизировать производительность при больших объемах данных или в реальном времени.
Вопрос-ответ:
Что такое сдвиг элементов массива вправо на Python?
Сдвиг элементов массива вправо — это операция, при которой каждый элемент массива перемещается на одну позицию вправо, а первый элемент переносится в конец массива. Эта операция полезна для решения различных задач, таких как циклические сдвиги, работы с очередями или определенные алгоритмы сортировки. В Python можно легко реализовать такой сдвиг с помощью срезов или метода `pop` и `insert`.