
Быстрая сортировка (QuickSort) – алгоритм, основанный на методе «разделяй и властвуй». В отличие от пузырьковой или сортировки вставками, QuickSort минимизирует количество операций обмена и эффективно работает даже с большими массивами. Средняя временная сложность – O(n log n), а в худшем случае – O(n²), если не использовать стратегию выбора опорного элемента.
Реализация алгоритма на Python обычно начинается с выбора опорного элемента (pivot). От этого выбора зависит баланс разбиения массива. В стандартных реализациях часто используют центральный элемент или случайный выбор. Далее список делится на две части: элементы меньше опорного и элементы больше либо равные. Каждая часть сортируется рекурсивно.
Важно избегать создания новых списков на каждом шаге, так как это увеличивает нагрузку на память. Эффективная реализация использует сортировку «на месте», изменяя исходный массив без создания дополнительных структур. Для этого применяются два указателя, которые сдвигаются навстречу друг другу, пока не найдут элементы, требующие обмена.
При практическом использовании QuickSort в Python стоит учитывать, что встроенная функция sorted() реализует гибридный алгоритм Timsort. Однако понимание механизма быстрой сортировки критически важно для оптимизации собственных алгоритмов и глубокого понимания работы с данными в Python.
Как выбрать опорный элемент в быстрой сортировке
Выбор опорного элемента (pivot) напрямую влияет на эффективность быстрой сортировки. Если выбрать его неудачно, особенно на уже отсортированных или частично отсортированных данных, алгоритм может деградировать до O(n²).
Оптимальные стратегии выбора pivot:
1. Серединный элемент
Быстро, но ненадёжно. Подходит только при случайных входных данных. Пример:
pivot = arr[len(arr) // 2]2. Первый или последний элемент
Простейший вариант, но не рекомендуется: при отсортированных входных данных сложность возрастает до квадратичной. Использовать стоит только для тестирования или в адаптированных алгоритмах с перестановками.
3. Случайный элемент
Позволяет избежать худших случаев при любом распределении входных данных. Требует генератора случайных чисел:
import random
pivot = arr[random.randint(0, len(arr) - 1)]4. Медиана трёх
Компромисс между скоростью и устойчивостью. Сравниваются первый, средний и последний элементы, выбирается медианный по значению:
mid = len(arr) // 2
pivot_candidates = [arr[0], arr[mid], arr[-1]]
pivot = sorted(pivot_candidates)[1]5. Медиана медиан
Используется в модификациях алгоритма с гарантированной O(n log n) сложностью. Затратно по времени, но эффективно при критичных к худшим случаям задачах (например, в системах реального времени).
Если нет жёстких требований по времени выполнения, медиана трёх обеспечивает хорошее соотношение надёжности и производительности. Для больших и непредсказуемых массивов – предпочтителен случайный выбор. Не выбирайте крайние элементы на реальных данных.
Что происходит при разбиении массива в Python
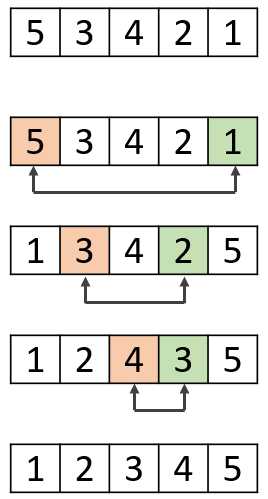
Разбиение – ключевой этап быстрой сортировки, где массив делится на две части относительно опорного элемента (pivot). В Python это реализуется с помощью указателей и сравнений. Выбор опорного элемента влияет на эффективность: лучший случай – средний элемент, худший – крайний.
Алгоритм начинается с выбора pivot, после чего элементы, меньшие pivot, перемещаются влево, большие – вправо. Это достигается с помощью двух индексов: один проходит по массиву, второй отслеживает границу элементов меньше pivot. При нахождении элемента, удовлетворяющего условию, выполняется обмен значений.
Пример: для массива [9, 3, 7, 1, 5] и pivot = 5 после разбиения получится [3, 1, 5, 9, 7], где 3 и 1 – слева от pivot, 9 и 7 – справа. Pivot занимает свою финальную позицию, после чего к каждой части рекурсивно применяется тот же алгоритм.
Для оптимизации рекомендуется избегать выбора крайних элементов в качестве pivot, особенно для почти отсортированных массивов. Эффективный подход – медиана трёх (первый, средний, последний элемент).
Рекурсивная реализация быстрой сортировки с примерами
Быстрая сортировка (QuickSort) реализуется с использованием принципа «разделяй и властвуй». Основная идея: выбрать опорный элемент, разделить список на элементы меньше и больше опорного, затем рекурсивно применить алгоритм к каждой части.
Рассмотрим реализацию на Python:
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
Этот вариант сохраняет неизменяемость входного массива, поскольку возвращает новый отсортированный список. Опорный элемент выбирается как центральный, что упрощает реализацию, но может негативно сказаться на производительности при уже отсортированных или частично отсортированных данных.
Для работы с большими объемами данных рекомендуется использовать модифицированную версию, в которой опорный элемент выбирается случайным образом:
import random
def quicksort_random(arr):
if len(arr) <= 1:
return arr
pivot = random.choice(arr)
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort_random(left) + middle + quicksort_random(right)
Такой подход снижает вероятность получения худшего случая с временной сложностью O(n²). Средняя сложность алгоритма сохраняется на уровне O(n log n), что делает его подходящим для большинства практических задач.
Важно учитывать, что рекурсивная реализация ограничена глубиной стека. Для обхода этой проблемы в Python можно увеличить предел рекурсии с помощью sys.setrecursionlimit(), однако предпочтительнее использовать итеративный вариант для массивов большой длины.
Обработка базового случая рекурсии
Быстрая сортировка использует рекурсию для разделения массива на подмассивы. Базовый случай останавливает дальнейшее рекурсивное деление, предотвращая бесконечный вызов функции.
- Базовым случаем является список длиной 0 или 1. Такой список уже отсортирован, и возвращается без изменений.
- Проверка выполняется в начале рекурсивной функции:
if len(arr) <= 1: return arr. - Эта проверка должна стоять строго перед выбором опорного элемента, чтобы не обращаться к несуществующим индексам при пустом списке.
- Отсутствие корректной обработки приводит к переполнению стека вызовов и аварийному завершению программы.
- Базовый случай не влияет на производительность в лучшем или худшем сценарии, но обеспечивает корректность работы алгоритма.
При написании рекурсивной функции важно гарантировать достижимость базового случая на каждом шаге. Например, при выборе опорного элемента и делении массива на подмассивы, хотя бы один из них должен уменьшаться по размеру.
Чем отличается внутренняя реализация от наглядной
Наглядная реализация быстрой сортировки в Python обычно демонстрируется с использованием рекурсии, случайного выбора опорного элемента и явного разделения массива на подмассивы. Примерно так:
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
Такая реализация проста, но неэффективна по памяти: она создаёт новые списки на каждом этапе, что увеличивает нагрузку на сборщик мусора и ограничивает производительность при работе с большими массивами.
Внутренние алгоритмы сортировки в Python, реализованные на C внутри функции list.sort() и sorted(), используют алгоритм Timsort – гибридную адаптивную сортировку, сочетающую элементы быстрой, вставочной и сортировки слиянием. Это позволяет избежать худшего случая O(n²), характерного для наивной быстрой сортировки, и использовать O(n) в лучшем случае при частично отсортированных данных.
Кроме того, внутренняя реализация не создаёт дополнительных списков и работает *на месте*, используя итерации вместо рекурсии, что исключает переполнение стека. Она также включает механизмы защиты от деградации производительности при неблагоприятных входных данных, чего нет в наглядной версии.
При разработке на Python для производственных задач предпочтительнее использовать встроенные методы сортировки, а не наглядные реализации, так как они оптимизированы по времени и памяти.
Как работает быстрая сортировка на списках с повторяющимися элементами

Основная идея быстрой сортировки заключается в том, чтобы выбрать опорный элемент, разделить список на две части: одну с элементами, меньшими опорного, и другую с элементами, большими опорного, а затем рекурсивно применить сортировку к каждой из этих частей. Когда в списке есть повторяющиеся элементы, важно правильно разделить их между подсписками.
- Если опорный элемент равен многим элементам списка, то из-за наличия повторений может возникнуть ситуация, когда одна из частей разделенного списка останется с минимальной длиной или вообще пустой. Это может привести к неэффективной работе алгоритма.
- Для предотвращения этого некоторые реализации быстрой сортировки используют стратегию разделения элементов равных опорному в отдельную группу, что снижает количество рекурсивных вызовов.
Процесс работы с повторяющимися элементами выглядит следующим образом:
- Выбор опорного элемента из списка. Он может быть любым элементом: первым, последним или медианой.
- Разбиение списка на три части: элементы, меньшие опорного, равные опорному и большие опорного. Такой подход позволяет сразу определить, что элементы, равные опорному, уже находятся на своем месте, и не требует дополнительных рекурсивных вызовов для этих элементов.
- Рекурсивная сортировка только для частей, содержащих элементы, меньшие или большие опорного.
При таком подходе, несмотря на наличие повторяющихся элементов, производительность быстрой сортировки не ухудшается и она остается достаточно эффективной с временной сложностью O(n log n). Однако, при слишком большом количестве одинаковых элементов можно столкнуться с ухудшением производительности, если не использовать модификации алгоритма.
Для ускорения работы с повторяющимися элементами стоит использовать следующие методы:
- Выбор более сбалансированного опорного элемента (например, медиану трех элементов), чтобы минимизировать вероятность наличия большого количества одинаковых элементов в одной из частей.
- Использование модификаций быстрой сортировки, таких как трехпартитное разбиение (с разделением на меньшее, равное и большее), что позволяет более эффективно обрабатывать повторяющиеся элементы.
Правильный выбор стратегии разбиения и опорного элемента играет ключевую роль в поддержании высокой производительности алгоритма, даже если в списке присутствуют повторяющиеся элементы.
Сравнение времени выполнения с сортировкой выбором
В отличие от сортировки выбором, быстрая сортировка использует стратегию «разделяй и властвуй», рекурсивно деля массив на две части вокруг опорного элемента. После чего каждая из частей сортируется независимо. Время выполнения быстрой сортировки в среднем составляет O(n log n), что значительно быстрее на практике, особенно при больших объёмах данных.
На практике быстрая сортировка значительно выигрывает у сортировки выбором. Для массивов, содержащих несколько сотен или тысяч элементов, быстрая сортировка выполняется заметно быстрее, с минимальными накладными затратами. При этом сортировка выбором может показаться даже неэффективной для массивов более 1000 элементов, так как время выполнения быстро растёт с увеличением размера массива.
Если рассматривать конкретные примеры, то для массива из 1000 элементов сортировка выбором может занять несколько секунд, в то время как быстрая сортировка справится с этим за доли секунды. Даже для массивов меньших размеров, например 100 элементов, быстрая сортировка обычно будет работать в несколько раз быстрее, хотя для таких маленьких наборов разница может быть не столь заметной.
Таким образом, быстрая сортировка является предпочтительным выбором для большинства задач, особенно когда важна скорость работы с большими массивами. Сортировка выбором может найти применение в учебных целях или для решения простых задач с небольшими объёмами данных, но она не подходит для производительных приложений.
Вопрос-ответ:
Что такое быстрая сортировка и как она работает на Python?
Быстрая сортировка (QuickSort) — это алгоритм сортировки, основанный на принципе «разделяй и властвуй». Алгоритм выбирает элемент из массива (обычно называют его опорным) и разделяет остальные элементы на два подмассива: один с элементами меньшими, чем опорный, и другой с элементами большими. Этот процесс повторяется рекурсивно для подмассивов до тех пор, пока все элементы не окажутся в отсортированном порядке. В Python быстрая сортировка реализована часто через рекурсию, что делает её удобной для использования в коде, несмотря на возможные ограничения по памяти из-за глубины рекурсии.
Как выбрать опорный элемент для быстрой сортировки?
В выборе опорного элемента нет единственного правильного подхода, и выбор может существенно повлиять на производительность алгоритма. Наиболее распространенные методы выбора опорного элемента — это выбор первого элемента, последнего, среднего элемента или случайного. Однако оптимальным вариантом считается использование медианы, так как это помогает сбалансировать массив и минимизировать вероятность худшего времени работы алгоритма. В реальных задачах часто используют случайный выбор опорного элемента для повышения эффективности в худших случаях, когда входные данные могут быть отсортированы или почти отсортированы.
Как быстрая сортировка работает с большими массивами данных в Python?
Сложность быстрой сортировки в среднем составляет O(n log n), что делает её довольно эффективной для сортировки больших массивов данных. Однако в худшем случае (например, если массив уже отсортирован) её сложность может быть O(n²). В Python это может стать проблемой из-за ограничений по глубине рекурсии, поскольку при большом числе рекурсивных вызовов программа может вызвать переполнение стека. Для работы с очень большими данными в Python рекомендуется использовать другие сортировки, такие как Timsort, которая используется в стандартной библиотеке Python и оптимизирована для реальных данных.
Какие преимущества и недостатки быстрой сортировки в Python?
Одним из главных преимуществ быстрой сортировки является её высокая производительность на случайных данных, где она показывает отличные результаты с временной сложностью O(n log n) в среднем. Это делает её подходящей для большинства практических задач, требующих сортировки больших объемов данных. Однако, у этого алгоритма есть и недостатки: в худшем случае его сложность может достигать O(n²), что делает его неэффективным для почти отсортированных массивов. Кроме того, из-за рекурсивного характера алгоритма, он может быть ограничен глубиной рекурсии, что при больших массивах может вызвать переполнение стека.






