В среде Wolfram Mathematica операция умножения матриц реализуется максимально лаконично – с использованием оператора .. Например, выражение A . B возвращает результат произведения двух матриц A и B, при условии, что число столбцов в первой матрице соответствует числу строк во второй. Ошибки при несоответствии размеров генерируются автоматически, что позволяет быстро диагностировать проблемы с исходными данными.
Особенность Mathematica – автоматическое приведение выражений к каноническому виду и поддержка символических вычислений. Это позволяет, например, умножать не только числовые, но и символьные матрицы без дополнительных преобразований. Запись {{a, b}, {c, d}} . {{x}, {y}} вернёт выражение {{a x + b y}, {c x + d y}}, что особенно полезно при работе с линейными преобразованиями и теоретическими выкладками.
Для многократного умножения используется функция Dot, которая автоматически интерпретирует скобки в нужном порядке. Пример: Dot[A, B, C] эквивалентен A . B . C и будет вычисляться последовательно слева направо. Это позволяет выполнять цепочки линейных преобразований без явной группировки и повышает читаемость кода.
Если требуется перемножить большие массивы данных, рекомендуется использовать функцию MatrixMultiply, так как она оптимизирована для работы с плотными и разреженными матрицами. При этом она также предоставляет доступ к дополнительным опциям, таким как транспонирование операндов до выполнения операции: MatrixMultiply[A, B, TransposeB → True].
Как задать матрицы для последующего умножения
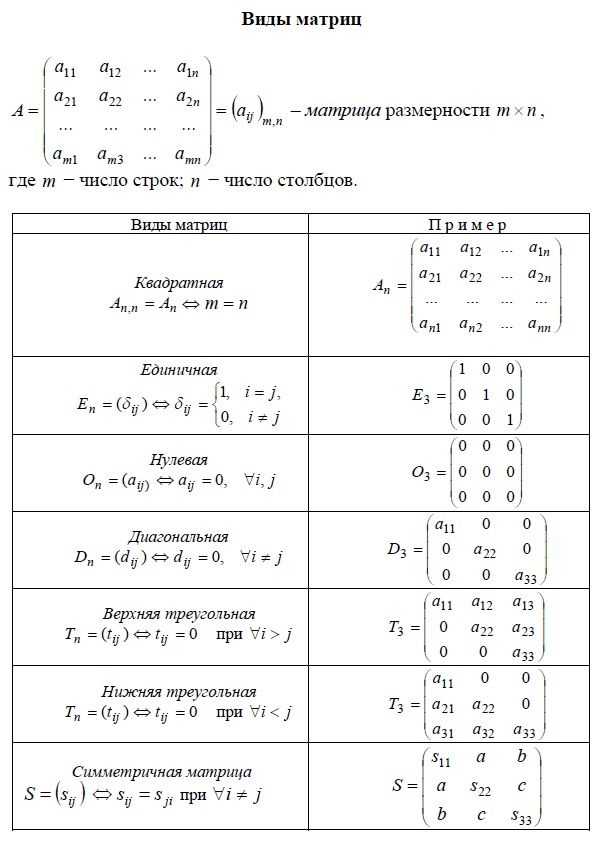
В Mathematica матрицы представляются в виде вложенных списков. Каждый внутренний список соответствует строке матрицы. Для создания матрицы необходимо использовать квадратные скобки и точную структуру вложенности.
Пример квадратной матрицы 3×3:
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
Для неквадратных матриц требуется строго соблюдать соответствие числу столбцов в первой матрице и числу строк во второй. Пример прямоугольной матрицы 2×3:
B = {{a, b, c}, {d, e, f}};
Чтобы упростить ввод больших матриц, используйте функцию Array. Например, создание матрицы 4×4 с элементами, зависящими от индексов:
M = Array[f, {4, 4}];
Если требуется конкретная матрица с числовыми элементами, можно задать значения с помощью встроенных функций, таких как RandomInteger:
RandomMatrix = RandomInteger[{0, 9}, {3, 3}];
Для проверки структуры используйте MatrixForm только для визуализации. Он не изменяет саму матрицу:
MatrixForm[A]
Использование оператора Dot для перемножения матриц
В Wolfram Mathematica оператор . (Dot) выполняет матричное умножение с точным соблюдением линейной алгебры. Он применим к двум и более матрицам, если выполняется условие совместимости размерностей: число столбцов в каждой левой матрице должно совпадать с числом строк в следующей правой.
Для перемножения двух матриц A и B используйте выражение A.B. Например:
A = {{1, 2}, {3, 4}};
B = {{5, 6}, {7, 8}};
A.B
Результат будет: {{19, 22}, {43, 50}}. Mathematica автоматически интерпретирует . как линейное произведение: строки первой матрицы умножаются на столбцы второй.
Dot поддерживает цепное умножение: A.B.C эквивалентно последовательному вычислению (A.B).C. Поскольку умножение ассоциативно, Mathematica может перестраивать порядок вычислений для оптимизации, но всегда соблюдает математическую корректность.
Оператор . также работает с векторами. Умножение строки на столбец возвращает скаляр (скалярное произведение), а столбца на строку – матрицу. Пример:
{1, 2, 3}.{4, 5, 6} (* Результат: 32 *)
{{1}, {2}, {3}}.{{4, 5, 6}} (* Результат: {{4, 5, 6}, {8, 10, 12}, {12, 15, 18}} *)
При работе с большими массивами Dot обеспечивает высокую производительность благодаря внутренней оптимизации. Для повышения эффективности избегайте преобразования матриц в списки вручную. Все входные данные должны быть в виде числовых массивов (матриц) без вложенных символов или выражений.
Используйте MatrixForm только для отображения, но не включайте его в вычисления: MatrixForm[A.B] визуализирует результат, но MatrixForm[A].MatrixForm[B] не выполняет умножение.
Умножение матриц с переменными и символами
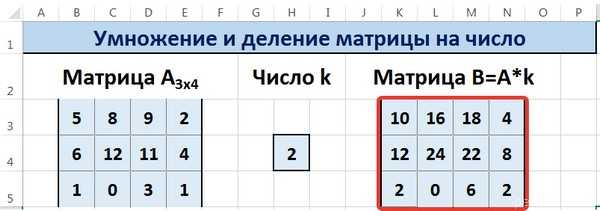
В Wolfram Mathematica работа с матрицами, содержащими символические выражения, позволяет проводить алгебраические преобразования без предварительной подстановки числовых значений. Это особенно полезно при аналитическом анализе систем уравнений, линейных преобразований и теоретических выкладках.
Для создания таких матриц используется функция {{a, b}, {c, d}} с произвольными символами. Умножение выполняется стандартной операцией .. Например:
A = {{a, b}, {c, d}};
B = {{x, y}, {z, w}};
A . BРезультатом будет матрица, содержащая выражения вида a*x + b*z, вычисленные согласно правилам матричного умножения. Mathematica не требует предварительного объявления переменных – они интерпретируются как символы по умолчанию.
MatrixForm[A . B]Если в выражениях заданы условия, такие как a > 0, они могут быть учтены в упрощении:
Assuming[a > 0, Simplify[A . B]]Чтобы гарантировать корректную интерпретацию символов как скаляров, а не как матриц или других объектов, полезно использовать функцию MatrixQ перед операцией умножения:
MatrixQ[A] && MatrixQ[B]При работе с символьными матрицами высокой размерности рекомендуется использовать Array с именованными элементами:
Array[a, {3, 3}]Это создаст матрицу {{a[1,1], a[1,2], a[1,3]}, ...}, что удобно для последующей подстановки или генерации систем уравнений. Для подстановки значений используйте ReplaceAll:
(A . B) /. {a -> 1, b -> 2}Работа с матрицами разного размера и проверка совместимости

Для умножения матриц в Wolfram Mathematica необходимо строго соблюдать правило: число столбцов в первой матрице должно совпадать с числом строк во второй. Нарушение этого условия приводит к сообщению об ошибке Dot::dotsh.
Чтобы проверить совместимость матриц A и B, используйте выражение Dimensions[A][[2]] == Dimensions[B][[1]]. Это сравнивает количество столбцов в первой матрице и количество строк во второй. Если выражение возвращает True, матрицы совместимы для умножения.
Для автоматизации процесса умножения и проверки можно использовать конструкцию:
If[Dimensions[A][[2]] == Dimensions[B][[1]], A.B, "Матрицы несовместимы"]
Если размерность одной из матриц заранее неизвестна, функцию MatrixQ можно использовать для валидации входных данных. Например:
If[MatrixQ[A] && MatrixQ[B], (* продолжить проверку и умножение *)]
Для работы с матрицами, созданными программно или загруженными из внешних источников, важно контролировать размерность через Dimensions сразу после загрузки. Это позволит избежать неявных ошибок при последующих операциях.
При использовании функций вроде RandomReal[{min, max}, {m, n}] важно четко задавать размеры, соответствующие правилам умножения. Например, чтобы умножить матрицу 3×4 на 4×2, используйте:
A = RandomReal[{0, 1}, {3, 4}];
B = RandomReal[{0, 1}, {4, 2}];
A.B
Для визуального контроля размеров можно использовать MatrixPlot и Dimensions в связке:
Grid[{Dimensions[#], MatrixPlot[#]} & /@ {A, B}]
Жесткое соблюдение размерностей и предварительная проверка совместимости позволяют избежать сбоев на этапе вычислений и автоматизировать обработку матриц различного происхождения.
Умножение нескольких матриц в одной строке
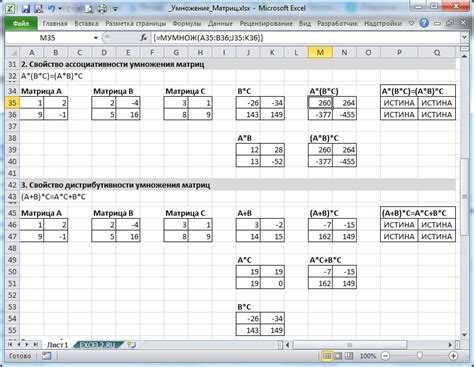
В Mathematica можно перемножать сразу несколько матриц, просто перечислив их через пробел внутри скобок. Используется обычное умножение . или встроенная функция Dot. Все операции происходят слева направо, с учетом размерностей.
A . B . CЗдесь A, B и C – матрицы с согласованными размерностями. Убедитесь, что:
- число столбцов предыдущей матрицы равно числу строк следующей,
- результат каждой промежуточной операции также подходит по размерности к следующему множителю.
Если переменные содержат численные матрицы, Mathematica выполнит все вычисления автоматически:
A = {{1, 2}, {3, 4}};
B = {{0, 1}, {1, 0}};
C = {{2, 0}, {0, 2}};
A . B . C
В результате произойдет последовательное умножение: сначала A . B, затем результат умножится на C. Использовать Dot можно также с Apply для работы со списком:
Dot @@ {A, B, C}Это особенно удобно, если количество матриц заранее неизвестно или они хранятся в списке.
MatrixForm[A . B . C]Избегайте применения MatrixForm внутри вычислений, так как это повлияет на результат, преобразуя выражения в формат отображения, а не вычисления.
Умножение матрицы на вектор

В Wolfram Mathematica операция умножения матрицы на вектор выполняется стандартным оператором умножения (звёздочкой) или функцией Dot. Матрица задаётся в виде списка списков, где каждый вложенный список – строка матрицы, а вектор – одномерным списком.
Пример умножения матрицы размером m×n на вектор длины n:
mat = {{a11, a12, ..., a1n}, ..., {am1, am2, ..., amn}};
vec = {v1, v2, ..., vn};
result = mat.vec;
Результат – вектор длины m, каждая компонента которого вычисляется как скалярное произведение соответствующей строки матрицы на вектор.
Обязательно проверяйте размерности: число столбцов матрицы должно совпадать с длиной вектора. Если размеры не согласованы, Mathematica выдаст ошибку.
Для повышения производительности при больших данных используйте функции Dot или оператор ., избегая циклов и ручного суммирования. Mathematica оптимизирует эти операции внутренне.
Если вектор – столбец (список списков с одним элементом в каждой вложенной списке), приведите его к одномерному списку с помощью Flatten или ArrayFlatten перед умножением.
Для многократных умножений на один и тот же вектор целесообразно использовать Compile для создания скомпилированной функции, что существенно ускорит вычисления.
Отладка ошибок при неправильном умножении матриц

Если возникает ошибка, связанная с несоответствием размеров, следует убедиться, что матрицы созданы и инициализированы правильно, а не как списки разной вложенности или одномерные массивы. Часто проблемы возникают при загрузке данных или преобразовании списков в матрицы.
Используйте встроенную функцию MatrixQ для проверки, что объекты действительно матрицы: MatrixQ[A]. Если результат False, необходимо привести структуру данных к двумерному виду или исправить ошибку в формировании матрицы.
Еще одна частая ошибка – использование операторов, не предназначенных для матричного умножения. В Mathematica умножение матриц выполняется через оператор Dot или сокращённо A.B. Попытка использовать обычное умножение A*B приведёт к поэлементному перемножению, что не всегда соответствует задаче.
Если необходимы операции с разреженными матрицами, убедитесь, что вы используете соответствующие функции, так как преобразование типов может влиять на совместимость операций.
Для детального анализа ошибок рекомендуется включить опцию Trace, которая позволяет отследить последовательность вычислений и выявить некорректные шаги: Trace[A.B].
Наконец, стоит избегать преобразования матриц к нестандартным типам данных без явного контроля, поскольку это может привести к скрытым ошибкам при умножении.
Вопрос-ответ:
Как выполнить умножение двух матриц в Wolfram Mathematica?
В Wolfram Mathematica для умножения матриц используется оператор двойного звездочки (**). Если заданы две матрицы A и B, их произведение можно получить выражением A.B или A ** B. При этом важно, чтобы число столбцов первой матрицы совпадало с числом строк второй.
Можно ли перемножить матрицы разных размеров в Mathematica, и как обработать ошибку несоответствия размерностей?
Перемножение матриц возможно только если количество столбцов первой матрицы равно количеству строк второй. Если размеры не подходят, Mathematica выдаст ошибку. Для проверки перед умножением можно использовать функцию Dimensions, чтобы сравнить размеры и избежать ошибки в процессе вычислений.
Как ускорить вычисление произведения больших матриц в Wolfram Mathematica?
Для работы с большими матрицами рекомендуется использовать встроенные оптимизации Mathematica, такие как SparseArray, если матрицы разреженные. Также можно использовать встроенные функции параллельных вычислений, например Parallelize, чтобы распределить операции умножения по нескольким ядрам процессора, что сокращает время расчёта.
Какие функции в Mathematica позволяют поэтапно контролировать умножение матриц?
Wolfram Mathematica предоставляет функции, с помощью которых можно вручную управлять умножением. Например, можно реализовать собственный алгоритм умножения с помощью Table и Sum для контроля над каждым элементом результата. Также полезна функция MapIndexed для применения операций к элементам матриц на определённых позициях.
Как проверить правильность результата умножения матриц в Wolfram Mathematica?
Для проверки результата умножения можно сравнить полученную матрицу с эталонным значением, используя функцию Equal (==). Также полезно проверить размер итоговой матрицы и убедиться, что каждый элемент совпадает с ожидаемым, особенно если вычисление было выполнено вручную через циклы или формулы.