Maple предоставляет точные инструменты для вычисления ряда Тейлора, позволяя аналитически представить функцию в виде степенного ряда. Этот процесс важен для аппроксимации сложных выражений, оптимизации вычислений и исследования поведения функций вблизи выбранной точки.
Основной командой для разложения является series, которая принимает три ключевых аргумента: функцию, точку разложения и порядок ряда. Правильный выбор этих параметров существенно влияет на точность и область применимости результата.
В ходе выполнения разложения рекомендуется поэтапно проверять промежуточные результаты – сначала вычислить производные вручную или с помощью Maple, затем сравнить их с коэффициентами ряда. Такой подход помогает выявить ошибки и понять структуру разложения.
Далее рассмотрим алгоритм действий в Maple, начиная с задания функции и параметров, заканчивая интерпретацией полученного результата, включая возможные ошибки и способы их устранения.
Выбор функции и постановка задачи в Maple
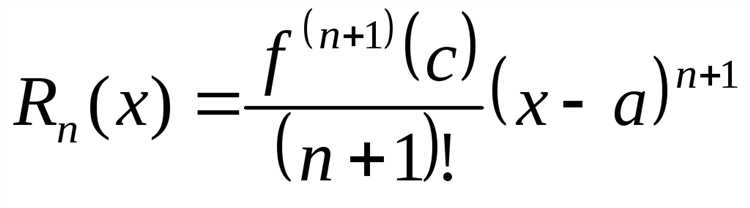
Для разложения функции в ряд Тейлора в Maple важно четко определить тип функции и область разложения. Maple корректно обрабатывает как элементарные функции (экспоненты, тригонометрические, логарифмы), так и сложные выражения, включая композиции и дробно-рациональные функции.
Перед началом необходимо задать функцию в синтаксисе Maple, используя оператор :=, например: f := x -> sin(x) * exp(x);. Обязательно указывать переменную, по которой будет выполняться разложение, чаще всего это x.
Следующий этап – выбор точки разложения. Обычно это точка 0 (ряд Маклорена) или любое другое значение a. В Maple это указывается в параметрах команды, например: series(f(x), x = a, n);, где n – порядок разложения.
Важный момент – определить порядок ряда с учетом целей задачи. Для приближенных расчетов достаточно порядка 3-5, для более точного анализа – 7 и выше. Maple позволяет легко менять этот параметр без переписывания всей функции.
Перед вычислением ряда рекомендуется проверить функцию на особенности: точки разрыва, особенности поведения около точки разложения, поскольку Maple выдаст предупреждения или неверные результаты при наличии сингулярностей.
Команда для вычисления ряда Тейлора в Maple

В Maple для разложения функции в ряд Тейлора используется команда series. Она позволяет получить приближенное выражение функции в виде степенного ряда вокруг заданной точки.
Синтаксис команды:
series(функция, переменная=точка, порядок)
Параметры:
функция– выражение, которое необходимо разложить.переменная– независимая переменная функции.точка– точка разложения, вокруг которой строится ряд (по умолчанию 0).порядок– максимальная степень переменной, до которой строится разложение (выражается как степень с плюсом, например, 6 означает до x^5 включительно, с остатком O(x^6)).
Пример для функции sin(x) в окрестности 0 с точностью до x⁵:
series(sin(x), x=0, 6);
Результат – разложение с членами до x⁵ и обозначением остаточного члена O(x^6).
Для разложения в окрестности точки x = a нужно явно указать точку:
series(f(x), x = a, n);
Если требуется получить полином Тейлора без остаточного члена, используют преобразование:
convert(series(функция, переменная=точка, порядок), polynom);
Важные рекомендации:
- Всегда указывайте точку разложения для контроля области аппроксимации.
- Порядок задавайте с учетом нужной точности, учитывая, что фактически вычисляются члены до степени на единицу меньше.
- Для функций нескольких переменных указывайте все переменные и точки разложения в списке.
Настройка точки разложения и порядка ряда в Maple

Для разложения функции в ряд Тейлора в Maple необходимо задать точку разложения и порядок ряда, что напрямую влияет на точность приближения и область сходимости. Точка разложения указывается как второй аргумент команды series, а порядок – третий. Например, запись series(f(x), x = a, n) разложит функцию f(x) в ряд Тейлора вокруг точки x = a с точностью до порядка n.
Точка разложения может быть любым числом или символическим значением, если требуется исследовать общий вид. При выборе точки стоит учитывать особенности функции – сингулярности или особенности поведения рядом с этой точкой могут ограничить применимость ряда. Если точка не указана, Maple по умолчанию использует разложение в окрестности нуля (x = 0).
Порядок ряда указывает, до какого степенного члена следует вычислять разложение. Важно выбирать порядок с учётом требуемой точности: слишком малый даст грубое приближение, слишком высокий – усложнит выражение и увеличит время вычисления. В Maple порядок указывается как целое число, равное максимальной степени разложения плюс один, то есть для разложения до степени 4 нужно указать n=5.
При необходимости построить ряд Тейлора в нескольких точках или с разными порядками рекомендуется создавать отдельные вызовы функции series с соответствующими параметрами. Для упрощения повторных вычислений удобно сохранять результаты в переменные.
Анализ полученного ряда и проверка точности приближения

После вычисления ряда Тейлора в Maple важно оценить адекватность разложения. Начните с визуального сравнения графиков исходной функции и полученного многочлена. В Maple используйте команду plot для наложения двух кривых на одном графике, задав одинаковый интервал.
Для количественной оценки точности вычислите остаточный член ряда или погрешность приближения. Maple позволяет определить разницу между функцией и суммой ряда с помощью команды simplify(f(x)-taylor_approx). Проанализируйте поведение погрешности на выбранном интервале, выделяя точки максимального отклонения.
Увеличение порядка разложения должно снижать ошибку. Проверьте динамику изменения максимальной ошибки при увеличении количества членов ряда с помощью цикла или последовательных вычислений. Если погрешность перестает уменьшаться, это может свидетельствовать о выходе за радиус сходимости или о необходимости использовать альтернативные методы приближения.
Для функций с особенностями (например, разрывами или неаналитическими точками) важно проверять, что ряд Тейлора построен именно в точке аналитичности, иначе точность может резко ухудшаться.
Для практических задач полезно определить минимальный порядок ряда, при котором погрешность не превышает заданный порог. В Maple можно реализовать автоматический подбор порядка, вычисляя ряд с увеличением степени до достижения нужной точности.
Резюмируя: анализ включает построение графиков, вычисление разницы функции и ряда, изучение поведения ошибки при увеличении числа членов и контроль области сходимости. Только такая комплексная проверка гарантирует адекватность и применимость разложения.
Визуализация функции и её ряда Тейлора в Maple
Для построения графика функции и её ряда Тейлора в Maple необходимо использовать команду plot совместно с вычислением ряда через series и преобразованием его в полином с помощью convert. Например, чтобы изобразить функцию f(x) = exp(x) и её ряд Тейлора порядка 5 в точке 0, сначала вычисляем ряд:
taylor_exp := convert(series(exp(x), x=0, 6), polynom);
Затем строим графики на одном полотне с помощью:
plot([exp(x), taylor_exp], x = -2 .. 2, legend = ["exp(x)", "Ряд Тейлора 5-го порядка"], color = [red, blue]);
Рекомендуется ограничить область построения вокруг точки разложения, так как ряд Тейлора точен вблизи этой точки, а дальше могут появляться большие расхождения.
Для визуального сравнения точности можно увеличивать порядок ряда, изменяя третий параметр в series. Maple позволяет строить несколько рядов одновременно, что удобно для анализа сходимости:
plots:-display([seq(convert(series(exp(x), x=0, n), polynom), n=2..7)], title = "Ряды Тейлора разного порядка");
Для улучшения читаемости графиков полезно добавлять легенды и задавать контрастные цвета. Если функция и её ряд сильно различаются, стоит сузить интервал x для фокусировки на окрестности точки разложения.
Визуализация ряда Тейлора помогает понять поведение приближения и оценить диапазон, в котором ряд адекватно отражает исходную функцию.
Сохранение и экспорт результатов разложения из Maple

print(серия_Тейлора, "filename.txt")
Для более структурированного хранения можно экспортировать выражение в формат MathML или LaTeX. Команда latex(серия_Тейлора) возвращает строку LaTeX, которую удобно вставлять в документы или редакторы с поддержкой TeX.
Для сохранения непосредственно в файл LaTeX применяйте функцию fprintf с открытым файловым дескриптором:
f := fopen("output.tex", WRITE): fprintf(f, "%s", latex(серия_Тейлора)): fclose(f);
Maple поддерживает экспорт в форматы Maple Worksheet (.mw) и Maple Input (.mpl). Для этого используйте меню «File» → «Export» и выберите нужный формат. Такой подход сохраняет как выражения, так и структуру сессии.
Если требуется дальнейшая обработка данных в других системах, можно сохранить результат как XML или JSON, преобразовав выражение в строку через export и специализированные пакеты, однако это требует дополнительной настройки.
Для быстрой передачи результатов в Excel применяйте экспорт через CSV, конвертируя численные коэффициенты ряда в массивы и сохраняя с помощью встроенных функций Maple.
Рекомендуется всегда проверять корректность сохраненного файла, открывая его в целевой программе. Для автоматизации экспорта можно создавать процедуры, инкапсулирующие команды сохранения с параметрами имени файла и формата.
Вопрос-ответ:
Как в Maple задать функцию для последующего разложения в ряд Тейлора?
В Maple функция вводится с помощью оператора присваивания, например: f := x -> sin(x)^2 + exp(x); После этого можно использовать команду для разложения, указывая переменную и точку разложения.
Какая команда в Maple отвечает за построение ряда Тейлора, и какие параметры она принимает?
Для разложения функции в ряд Тейлора используется команда taylor(f(x), x = a, n), где f(x) — функция, x — переменная, a — точка, около которой строится ряд, а n — порядок разложения. Например, taylor(sin(x), x=0, 5) выдаст ряд Тейлора для синуса с точностью до x^4.
Можно ли получить в Maple разложение с остаточным членом, и как это сделать?
Да, Maple позволяет выводить разложение с остаточным членом, используя параметр ‘rest’. Команда выглядит так: taylor(f(x), x = a, n, ‘rest’). Это даст выражение ряда с явным обозначением остаточного члена, который показывает погрешность аппроксимации.
Как в Maple визуально сравнить функцию и её разложение в ряд Тейлора на графике?
Можно построить график функции и её приближенного разложения с помощью команды plot. Например, plot([f(x), taylor(f(x), x=a, n)], x = xmin..xmax) выведет оба графика на одном рисунке для сравнения поведения исходной функции и её приближения.
Какие особенности следует учитывать при выборе точки и порядка разложения в Maple для ряда Тейлора?
Выбор точки разложения влияет на область точного приближения: обычно выбирают точку, близкую к интересующему диапазону. Порядок ряда определяет точность — больше порядок даёт лучшее приближение, но увеличивает вычислительную нагрузку. В Maple можно экспериментировать с этими параметрами, наблюдая изменение результата и графиков.
Как в Maple найти разложение заданной функции в ряд Тейлора и какие команды для этого использовать?
Для получения разложения функции в ряд Тейлора в Maple применяется команда `series`. Нужно задать функцию, указать точку разложения и порядок ряда. Например, чтобы разложить функцию \( \sin(x) \) около точки 0 до порядка 6, вводят: `series(sin(x), x=0, 6)`. Maple выдаст приближённое выражение в виде суммы степеней \(x\) с коэффициентами. Важно понимать, что точка разложения и порядок влияют на точность и вид результата. После вычисления можно использовать команду `convert` с параметром `polynom`, чтобы получить полином без хвостового члена.
Можно ли получить в Maple разложение функции в ряд Тейлора с шагом вычисления каждого члена и как это сделать?
Да, Maple позволяет выполнять разложение с подробным отображением промежуточных шагов. Для этого можно использовать команды дифференцирования и подстановки значений вручную. Сначала вычисляют производные функции в выбранной точке, затем подставляют их в формулу Тейлора. При желании, можно написать простой скрипт, который автоматически будет вычислять члены ряда, показывая процесс пошагово. Это полезно для понимания, как формируются коэффициенты и степень каждого слагаемого. Однако готовой команды, которая выводит именно «пошагово» все вычисления, в стандартных инструментах Maple нет — приходится строить такие действия самостоятельно, используя функции дифференцирования (`diff`) и подстановки (`subs`).