Как решать интегралы mathcad

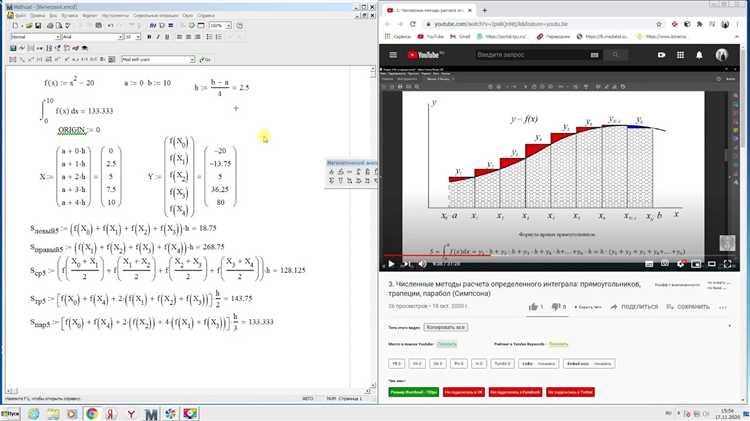
Mathcad предоставляет эффективные инструменты для вычисления интегралов, объединяя аналитические и численные методы. Важно понимать разницу между встроенными функциями символического интегрирования и численными алгоритмами, чтобы выбирать оптимальный подход для конкретной задачи.

Для аналитического решения Mathcad использует движок Maple, который позволяет получать точные выражения интегралов. При этом корректное определение переменных, границ интегрирования и условий непрерывности функции существенно повышает качество результата.

Численные методы в Mathcad, такие как метод трапеций и метод Симпсона, применяются при невозможности получить аналитическое выражение или при работе с экспериментальными данными. Настройка точности и разбиения интервала играет ключевую роль в достижении приемлемой погрешности.

В статье представлен подробный разбор команд Mathcad для интегрирования, включая их параметры и примеры использования. Такой подход позволяет не только выполнить вычисления, но и контролировать каждый этап, анализируя промежуточные результаты.

Как настроить Mathcad для работы с определёнными и неопределёнными интегралами

Для корректного вычисления интегралов в Mathcad необходимо задать переменные, функцию и границы интегрирования, если речь идёт об определённом интеграле. В первую очередь убедитесь, что переменные объявлены как скалярные, иначе Mathcad может воспринимать их как массивы, что приведёт к ошибкам.

Для неопределённых интегралов используйте встроенную функцию int в форме int(выражение, переменная). Например, int(x^2, x) вычислит неопределённый интеграл функции x². Обратите внимание, что Mathcad автоматически добавляет константу интегрирования.

Для определённых интегралов применяется расширенный синтаксис int(выражение, переменная, нижний_предел, верхний_предел). Важно задавать числовые значения или переменные с определёнными значениями в пределах, иначе результат останется в символьной форме.

Перед вычислением проверьте тип переменных с помощью функции typeof, чтобы исключить несоответствия. При работе с параметрическими интегралами определите параметры отдельно, задав их численные значения заранее.

В настройках документа активируйте поддержку символьных вычислений, чтобы Mathcad мог выполнять аналитическое интегрирование, а не только численное. Это особенно важно для сложных функций с переменными пределами.

Для повышения точности численного интегрирования используйте функцию evalf и задавайте необходимое количество значимых цифр через precision. Это позволит избежать погрешностей, возникающих при автоматическом округлении.

Пошаговое вычисление неопределённого интеграла в Mathcad с примерами

В Mathcad вычисление неопределённого интеграла происходит с помощью встроенных функций и интерактивных инструментов. Для точного результата важна правильная последовательность действий.

1. Определите функцию для интегрирования. Введите выражение функции в рабочую область, например: f(x) := sin(x)^2 + 3*x.
2. Вызовите оператор интегрирования. В Mathcad используется оператор ∫ (на панели операторов или с помощью комбинации клавиш). Для неопределённого интеграла напишите: F(x) := ∫ f(x) dx.
3. Проверьте корректность переменной интегрирования. Переменная в операторе dx должна совпадать с переменной функции. Ошибка здесь приведёт к неверному результату.
4. Получите результат. Mathcad автоматически вычислит первообразную, отображая выражение с константой интегрирования + C, например: F(x) = -cos(x)*sin(x)/2 + (3*x^2)/2 + C.
5. Используйте дополнительные команды для упрощения. Если результат сложен, примените функцию simplify() или expand() для упрощения и раскрытия скобок.

Пример 1. Найти неопределённый интеграл функции f(x) := e^(2*x) * cos(x).

1. Ввод: f(x) := exp(2*x)*cos(x).
2. Вычисление: F(x) := ∫ f(x) dx.
3. Mathcad выдаст результат в виде суммы экспонент и тригонометрических функций с константой C.
4. При необходимости: simplify(F(x)) для более компактного выражения.

Пример 2. Интегрирование полинома g(t) := 4*t^3 - 2*t + 7.

1. Ввод: g(t) := 4*t^3 - 2*t + 7.
2. Вычисление: G(t) := ∫ g(t) dt.
3. Ожидаемый результат: G(t) = t^4 - t^2 + 7t + C.

Использование численных методов для интегрирования сложных функций в Mathcad

Mathcad предоставляет эффективные инструменты для численного интегрирования, особенно когда аналитическое решение затруднено или невозможно. Для интегрирования функций с нестандартными выражениями, особыми точками разрыва или сложными зависимостями рекомендуется применять встроенную функцию int() с указанием интервала интегрирования.

Численное интегрирование в Mathcad основано на методах квадратур, в частности на методе Симпсона и методе трапеций, которые автоматически выбираются в зависимости от параметров задачи. Для повышения точности следует задавать явные границы интегрирования и контролировать шаг разбиения, изменяя параметры функции или используя разбиение на подынтервалы.

При вычислении интегралов от функций с осциллирующим или быстро изменяющимся поведением полезно разбивать интервал на несколько частей и интегрировать каждую отдельно, а затем суммировать результаты. Это снижает накопление численных ошибок и улучшает сходимость.

В Mathcad возможно использовать оператор «присвоения» с циклом для реализации собственных алгоритмов численного интегрирования, например, метода прямоугольников или метод Монте-Карло, если стандартные средства не обеспечивают необходимой точности.

Для контроля погрешности рекомендуется сравнивать результаты интегрирования с уменьшенным шагом или использовать встроенные функции оценки ошибки. В случае необходимости интегрирования по бесконечным или полуинтервалам применяются преобразования переменной с последующим численным вычислением на конечных интервалах.

Автоматическое упрощение результатов интегрирования и работа с константами

Mathcad автоматически упрощает выражения, полученные после интегрирования, используя встроенные алгоритмы символьной алгебры. Однако уровень упрощения зависит от исходной формы функции и настроек документа. Для повышения читаемости результата рекомендуется применять функцию simplify(), которая устраняет избыточные множители, преобразует выражения в более компактные формы и раскрывает скобки.

При вычислении неопределённых интегралов Mathcad добавляет константу интегрирования в виде параметра (например, C0). Пользователь может задать имя этой константы вручную, чтобы избежать путаницы в больших вычислениях, используя опцию Constants в настройках интегратора.

Если результат интегрирования содержит параметры или константы, допускается последующее упрощение с помощью команд expand() или factor(), что помогает выявить скрытые зависимости или привести выражение к стандартному виду.

Для численного интегрирования с последующей символической обработкой полезно разделять вычисление значения интеграла и упрощение результата. Это предотвращает нежелательное округление и сохраняет точность аналитической формы.

При работе с определёнными интегралами Mathcad автоматически подставляет пределы интегрирования и упрощает полученную разность. В случае сложных выражений рекомендуется вручную проверить результат с помощью simplify() и при необходимости использовать assume() для задания ограничений на переменные, что улучшит качество упрощения.

Вычисление кратных интегралов: инструкция для Mathcad

Mathcad позволяет эффективно вычислять кратные интегралы, используя встроенные функции и корректно задавая пределы интегрирования. Для работы с двойными и тройными интегралами применяется функция int с несколькими переменными.

1. Объявите переменные интегрирования. Например, для двойного интеграла по переменным x и y используйте:
   • x:=0..1 – диапазон изменения x
   • y:=0..2 – диапазон изменения y
2. Определите функцию под интегралом. Например, f(x,y):=x^2 + y^2.
3. Задайте двойной интеграл с помощью встроенной функции:
   • int(int(f(x,y), x, x0, x1), y, y0, y1)
   • Здесь x0, x1 и y0, y1 – числовые пределы интегрирования.
4. Для переменных с зависящими пределами используйте выражения вместо чисел:
   • Например, int(int(f(x,y), x, 0, y), y, 0, 1) – интеграл по области, где x изменяется от 0 до y.
5. Для тройных интегралов применяйте вложенную функцию int:
   • int(int(int(f(x,y,z), x, x0, x1), y, y0, y1), z, z0, z1)
   • Где f(x,y,z) – функция трех переменных, а пределы определены аналогично.
6. Используйте численные методы для сложных функций или областей:
   • Если аналитическое интегрирование невозможно, Mathcad вычисляет численный результат автоматически.
   • При необходимости повысить точность, укажите параметр точности в настройках функции int.
7. Для проверки результата визуализируйте функцию и область интегрирования с помощью графиков Mathcad.

Обратите внимание, что пределы интегрирования должны быть корректно оформлены, включая зависимые переменные. Неправильно заданные пределы приводят к ошибкам или неверным результатам.

Решение интегралов с параметрами и переменными в Mathcad

Mathcad позволяет вычислять определённые и неопределённые интегралы, содержащие параметры и переменные, используя встроенные функции и операторы. Для интеграла с переменными и параметрами в Mathcad важно корректно определить область интегрирования и задать все параметры как числовые или символические значения.

При интегрировании функции с параметрами следует использовать оператор интеграла ∫, вводимый через панель математических символов или команду int. Важно, чтобы параметры были объявлены заранее и имели числовые значения, иначе Mathcad выполнит интегрирование в символическом виде.

Пример: для функции f(x) = a*x^2 + b с параметрами a и b нужно определить значения параметров, например a:=2, b:=1, затем вычислить интеграл ∫ f(x) dx или определённый интеграл ∫_0^1 f(x) dx. Mathcad автоматически подставит параметры и вычислит результат.

Для интегралов с переменными верхнего и нижнего пределов можно использовать переменные вместо конкретных чисел, что позволяет проводить численное интегрирование при изменении границ. При этом границы задаются через присваивание переменным и используются в команде интеграла: ∫_{c}^{d} f(x) dx, где c и d – переменные.

Если параметры остаются символическими, Mathcad возвращает выражение в аналитическом виде. Для перехода к численному результату нужно использовать функцию eval или заменить параметры на числовые значения перед вычислением.

Рекомендуется при работе с параметрическими интегралами использовать разделение определения параметров и вычисления интеграла в разных блоках для наглядности и удобства изменения значений. Это повышает гибкость и снижает вероятность ошибок.

Отладка и проверка правильности вычисленных интегралов в Mathcad

Для проверки производной интеграла используйте оператор дифференцирования diff. Производная от неопределённого интеграла должна совпадать с исходной подынтегральной функцией. Несовпадение укажет на ошибку в записи или вычислении.

Если интеграл вычисляется численно, увеличьте точность вычислений, задав меньший шаг сетки в параметрах функции int или используя встроенные настройки численной интеграции. Сравните результаты при различных настройках для оценки устойчивости.

Используйте альтернативные методы интегрирования в Mathcad, например, замену переменных или разложение подынтегральной функции в ряд, чтобы получить независимые результаты. Их сопоставление выявит возможные ошибки.

При работе с параметрическими интегралами задавайте фиксированные значения параметров и сверяйте результаты с ручным расчетом или проверенными аналитическими формулами. Это эффективно для выявления систематических ошибок.

Для сложных выражений применяйте функцию simplify(), чтобы привести полученное интегральное выражение к более компактному виду. Часто упрощение выявляет несоответствия и позволяет легче проводить проверку.

Обязательно проверяйте единицы измерения результата, если используются физические величины. Несоответствие единиц указывает на ошибку в постановке задачи или вводе данных.

Вопрос-ответ:

Какие основные способы решения интегралов поддерживаются в Mathcad?

В Mathcad реализованы разные подходы к вычислению интегралов: численное интегрирование, аналитическое решение с помощью встроенных функций, а также разложение выражений и использование правил интегрирования. Программа позволяет пошагово показать ход решения, что помогает понять, какие операции выполняются на каждом этапе.

Как в Mathcad выполнить пошаговое интегрирование неопределённого интеграла?

Для пошагового решения неопределённого интеграла в Mathcad нужно задать функцию, вызвать команду интегрирования, а затем активировать режим показа промежуточных этапов. В результате вы увидите последовательность преобразований — применение формул интегрирования, замены переменных и упрощения выражений. Такой подход помогает лучше понять логику вычислений и проверить корректность каждого шага.

В чем разница между численными и аналитическими методами интегрирования в Mathcad?

Аналитические методы позволяют получить точное выражение первообразной функции, используя известные формулы и таблицы интегралов. Численные методы, такие как метод трапеций или Симпсона, дают приближённый результат для сложных функций или при отсутствии точного решения. Mathcad предлагает оба варианта: аналитические решения хорошо подходят для учебы и проверки, а численные — для практических расчетов, когда точная формула не находится.

Можно ли в Mathcad решать интегралы с параметрами и как отображается зависимость от них?

Да, Mathcad умеет работать с интегралами, содержащими параметры. При введении переменных в функцию интегрирования программа позволяет сохранить параметр в выражении и вывести результат в виде функции от этого параметра. Это удобно для анализа, как меняется значение интеграла при различных значениях параметра, а также для построения графиков зависимости.

Какие ошибки часто встречаются при вводе интегралов в Mathcad и как их избежать?

Часто допускаемые ошибки связаны с неправильным оформлением выражения, например, пропущенные скобки, неверный формат записи функции или ошибка в обозначении переменной интегрирования. Чтобы минимизировать такие проблемы, рекомендуется использовать подсказки и шаблоны Mathcad, внимательно проверять синтаксис и запускать предварительный анализ выражения. Кроме того, полезно внимательно изучить результаты промежуточных шагов, чтобы вовремя заметить несоответствия.

Какие основные способы решения интегралов доступны в Mathcad, и как их использовать пошагово?

В Mathcad есть несколько подходов к вычислению интегралов: аналитический и численный. Аналитический метод предполагает использование встроенных функций для нахождения точного выражения первообразной. Для этого достаточно ввести интеграл с помощью оператора интегрирования и нажать вычислить. Если аналитическое решение невозможно или слишком сложное, Mathcad позволяет применить численное интегрирование — метод, при котором интеграл приближенно вычисляется по значениям функции на выбранном отрезке. Обычно это делается с помощью команд, указывающих пределы интегрирования и требуемую точность. В статье подробно расписан каждый из этих методов с примерами и объяснениями шагов, что помогает понять, когда и как использовать подходящий способ.