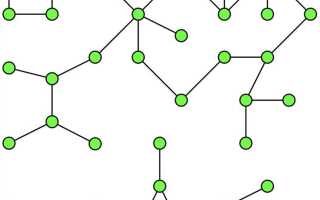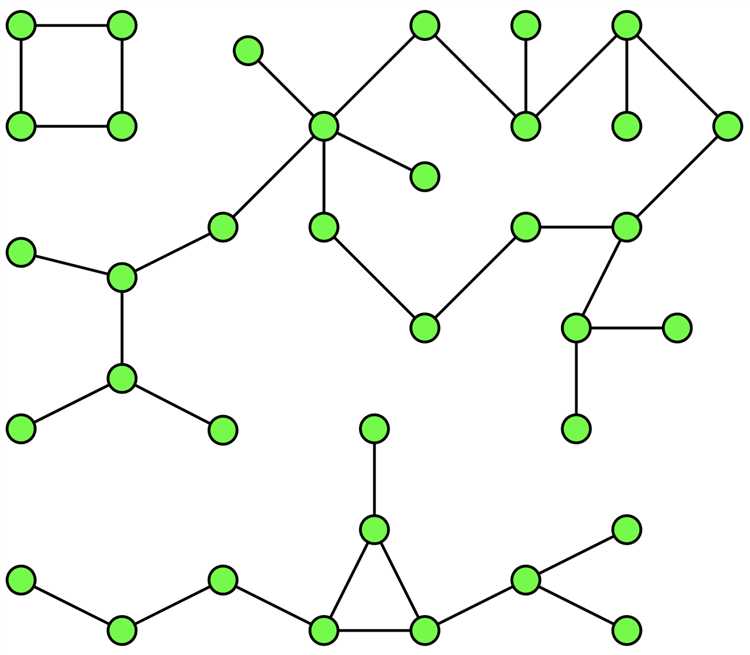
Графы – это мощный инструмент для моделирования и анализа взаимосвязей в различных областях: от социальных сетей до биоинформатики и логистики. В Python создание и визуализация графов стали доступными благодаря широкому набору библиотек, таких как NetworkX, Matplotlib, и Plotly. Эти инструменты позволяют не только построить граф, но и представить его в удобной и информативной форме, облегчая анализ данных и выявление закономерностей.
Для начала работы с графами в Python важно понимать их структуру. В отличие от традиционных коллекций данных, граф состоит из вершин (или узлов) и рёбер, соединяющих эти вершины. В Python реализация графов часто сводится к использованию словарей или списков для хранения рёбер и вершин. Одной из популярных библиотек для работы с графами является NetworkX, которая предоставляет простой API для создания, манипулирования и визуализации графов.
После того как граф построен, его визуализация играет ключевую роль в понимании структуры и характеристик сети. Для этих целей можно использовать Matplotlib, которая хорошо интегрируется с NetworkX, или более современные решения, такие как Plotly, для создания интерактивных графиков. Визуализация графов помогает выявить такие важные характеристики, как центральность, плотность сети, и влияние отдельных узлов, что в свою очередь может быть полезно при решении задач анализа данных или оптимизации.
Создание графов с помощью библиотеки NetworkX
Для начала работы с NetworkX необходимо установить её с помощью команды:
pip install networkx
После этого можно приступать к созданию графов.
Создание простого графа
Чтобы создать простой неориентированный граф, достаточно использовать класс Graph:
import networkx as nx G = nx.Graph()
Граф будет пустым, и для добавления узлов и рёбер нужно использовать соответствующие методы:
add_node()– добавление узла;add_edge()– добавление ребра между двумя узлами.
Пример создания графа с двумя узлами и одним рёбером:
G.add_node(1) G.add_node(2) G.add_edge(1, 2)
Добавление нескольких узлов и рёбер
Для добавления сразу нескольких узлов и рёбер можно использовать методы add_nodes_from() и add_edges_from(). Например:
G.add_nodes_from([3, 4, 5]) G.add_edges_from([(2, 3), (3, 4)])
В результате получится граф с пятью узлами и тремя рёбрами.
Работа с направленными графами
Для создания направленного графа используется класс DiGraph. В этом случае рёбра будут иметь направление:
DG = nx.DiGraph() DG.add_edge(1, 2) # Ребро направлено от узла 1 к узлу 2
Взвешенные графы

NetworkX поддерживает создание взвешенных графов, где рёбра могут иметь веса. Для добавления веса к рёбрам используется параметр weight:
G.add_edge(1, 2, weight=4.2)
Чтобы получить вес рёбера, можно использовать метод get_edge_data():
G.get_edge_data(1, 2)
Визуализация графов
NetworkX интегрируется с библиотеками для визуализации, например, matplotlib. Для отрисовки графа достаточно вызвать функцию nx.draw():
import matplotlib.pyplot as plt nx.draw(G, with_labels=True) plt.show()
Для более сложных визуализаций можно настроить параметры, такие как цвет узлов, стиль рёбер и шрифты меток.
Работа с большими графами
При работе с большими графами важно учитывать эффективность. NetworkX предоставляет методы для оптимизации использования памяти и вычислительных ресурсов. Например, можно использовать MultiGraph для графов с несколькими рёбрами между узлами, а также работать с подграфами и динамическим добавлением рёбер.
С помощью библиотеки NetworkX можно легко строить сложные графовые структуры, анализировать их и визуализировать, что делает её незаменимым инструментом для работы с графами в Python.
Как добавить узлы и рёбра в граф
Для добавления узлов и рёбер в граф в Python можно использовать библиотеку NetworkX, которая предоставляет удобные методы для работы с графами. Основные операции добавления узлов и рёбер просты и интуитивно понятны. Рассмотрим, как это сделать шаг за шагом.
1. Добавление узлов осуществляется с помощью метода add_node(). Если необходимо добавить несколько узлов, можно использовать метод add_nodes_from(). Важно заметить, что узлы в NetworkX могут быть любыми объектами: числами, строками, кортежами и так далее.
import networkx as nx
G = nx.Graph()
G.add_node(1) # Добавление одного узла
G.add_nodes_from([2, 3, 4]) # Добавление нескольких узлов
2. Рёбра добавляются с помощью метода add_edge(). Этот метод принимает два параметра – идентификаторы узлов, между которыми будет добавлено ребро. Если необходимо добавить сразу несколько рёбер, можно воспользоваться add_edges_from().
G.add_edge(1, 2) # Добавление ребра между узлами 1 и 2
G.add_edges_from([(2, 3), (3, 4)]) # Добавление нескольких рёбер
3. Дополнительные атрибуты можно добавлять к узлам и рёбрам с помощью параметров. Например, атрибуты могут быть полезны для хранения дополнительной информации, связанной с каждым элементом графа.
G.add_node(5, label="new_node", weight=4) # Узел с аттрибутами
G.add_edge(1, 5, weight=2, color="red") # Ребро с аттрибутами
4. Важно понимать, что в неориентированных графах рёбра не имеют направления. Для ориентированных графов используется класс DiGraph, и рёбра добавляются с учетом направления.
DG = nx.DiGraph()
DG.add_edge(1, 2) # Ориентированное ребро от узла 1 к узлу 2
Таким образом, добавление узлов и рёбер – это основные операции при построении графа в Python с использованием библиотеки NetworkX. Комбинируя эти методы, можно эффективно строить и манипулировать графами различной сложности.
Выбор алгоритмов для работы с графами: краткие пути, кластеризация
Для нахождения кратчайших путей на графах наиболее часто используются два алгоритма: алгоритм Дейкстры и алгоритм Беллмана-Форда. Алгоритм Дейкстры эффективен при наличии графа с неотрицательными весами рёбер. Его сложность составляет O(V log V + E), где V – количество вершин, E – количество рёбер. Он находит кратчайшие пути от одной вершины до всех остальных. Алгоритм Беллмана-Форда, в отличие от Дейкстры, работает и с графами, содержащими рёбра с отрицательными весами. Однако его сложность выше – O(VE), что делает его менее эффективным для больших графов. Для поиска кратчайших путей между всеми парами вершин можно использовать алгоритм Флойда-Уоршелла, который имеет временную сложность O(V³), но позволяет эффективно обрабатывать все возможные пути между вершинами графа.
Для задач кластеризации графов используются алгоритмы, такие как алгоритм Краскала и алгоритм Прима. Оба алгоритма предназначены для построения минимального остовного дерева (MST) графа. Алгоритм Краскала эффективен для разреженных графов, так как использует структуру данных «система непересекающихся множеств», что позволяет реализовать его с временной сложностью O(E log E), где E – количество рёбер. Алгоритм Прима больше подходит для плотных графов, так как его сложность составляет O(E + V log V), где V – количество вершин. Для поиска кластеров в графах с учетом их структуры могут быть использованы также методы спектральной кластеризации, которые применяют собственные значения матрицы смежности графа.
Таким образом, выбор алгоритма зависит от конкретной задачи и характеристик графа. Для задачи нахождения кратчайших путей важны такие аспекты, как наличие отрицательных весов рёбер и необходимость нахождения путей между всеми парами вершин. Для кластеризации важным фактором является плотность графа и тип задачи, от чего зависит выбор между алгоритмами для построения минимального остовного дерева и методами спектральной кластеризации.
Визуализация графов с использованием Matplotlib

Для визуализации графов в Python часто используется библиотека Matplotlib. Она позволяет легко создавать графические представления для различных типов данных, включая графы. В комбинации с библиотеками, такими как NetworkX, Matplotlib становится мощным инструментом для отображения структуры графов.
Основные шаги для построения графа с использованием Matplotlib:
- Создание графа: Для начала создайте объект графа с помощью библиотеки NetworkX.
- Рисование графа: Используйте функции NetworkX для отображения графа, например,
nx.draw(), с параметрами, которые можно настроить для улучшения визуализации. - Настройка параметров визуализации: Можно настроить цвет, размер, форму узлов и ребер, а также шрифты для меток.
- Отображение графа: Воспользуйтесь функцией
plt.show()из Matplotlib для отображения конечного результата.
Пример простого кода для создания и визуализации графа:
import matplotlib.pyplot as plt import networkx as nx # Создание графа G = nx.erdos_renyi_graph(10, 0.3) # Визуализация графа nx.draw(G, with_labels=True, node_color='skyblue', node_size=800, font_size=12, font_weight='bold') # Отображение plt.show()
В этом примере создается случайный граф с 10 узлами и вероятностью соединения 0.3. Узлы отображаются в голубом цвете, их размер установлен на 800, а шрифт для меток узлов — на 12.
Для улучшения визуализации графа можно использовать различные опции:
node_size: Определяет размер узлов. Для крупных графов это важно для предотвращения наложения узлов.node_color: Позволяет задать цвет узлов, что может помочь в визуальном разделении различных групп узлов.edge_color: Задает цвет ребер, что полезно при отображении различных типов связей.pos: Для детальной настройки расположения узлов. Множество алгоритмов, таких какspring_layout,circular_layout, позволяют контролировать положение узлов на графике.
Пример с расположением узлов с использованием spring_layout:
pos = nx.spring_layout(G) nx.draw(G, pos, with_labels=True, node_color='lightgreen', edge_color='gray', node_size=700) plt.show()
Для анализа графа можно также добавлять аннотации, отображать веса на ребрах и создавать интерактивные визуализации, комбинируя Matplotlib с другими библиотеками, такими как Plotly или Pyvis. Но в большинстве случаев Matplotlib является достаточным инструментом для визуализации стандартных графов.
Настройка внешнего вида графа: цвета, размер узлов и рёбер
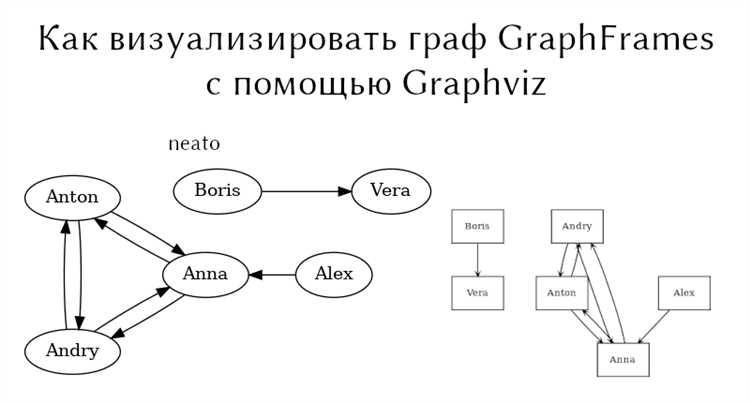
Для улучшения восприятия графов в Python можно настроить внешний вид узлов и рёбер. Это позволяет выделить важные элементы или создать более эстетически привлекательные визуализации. В библиотеке NetworkX настройки внешнего вида производятся через параметры, передаваемые в функции отображения графа. Рассмотрим, как настроить цвета, размеры узлов и рёбер.
Цвета узлов и рёбер: Параметр node_color позволяет задать цвет всех узлов в графе. Вы можете использовать стандартные цвета (например, ‘red’, ‘blue’, ‘green’) или передать список цветов, если нужно задать разные цвета для разных узлов. Например, если у вас есть список значений, можно использовать их для динамического выбора цветов в зависимости от каких-либо характеристик узлов.
Для рёбер используется параметр edge_color, аналогично для узлов. Если необходимо задать цвет рёбер в зависимости от их веса или другой метрики, можно передать список цветов, соответствующих каждому ребру. Например, рёбра с большим весом можно выделить более ярким цветом, что улучшит восприятие данных.
Размер узлов: Для изменения размера узлов используется параметр node_size. Он принимает либо одно число, чтобы задать размер всех узлов, либо список чисел для каждого узла. Размер узлов часто зависит от их степени или веса. Для этого можно вычислить степень каждого узла с помощью networkx.degree() и передать соответствующие значения в параметр node_size.
Размер рёбер: В NetworkX можно также настроить толщину рёбер с помощью параметра width. Если вы хотите, чтобы рёбра с большим весом были толще, передайте список значений, соответствующих весам рёбер. Это позволит зрительно выделить важные рёбра, что особенно полезно при анализе графов с большим количеством узлов и рёбер.
Важно помнить, что чрезмерное использование ярких цветов и больших узлов может привести к перегрузке визуализации. Рекомендуется выбирать такие настройки, которые подчеркивают структуру графа и позволяют быстро ориентироваться в данных.
Оптимизация работы с большими графами в Python
Для эффективной работы с большими графами в Python необходимо учитывать несколько ключевых аспектов, таких как представление графа в памяти, алгоритмы обхода и поиска, а также использование специализированных библиотек. Большие графы требуют оптимизации как по памяти, так и по скорости обработки. Рассмотрим несколько методов оптимизации.
Первый шаг – выбор правильной структуры данных. Для хранения графов чаще всего используют два подхода: список смежности и матрицу смежности. Список смежности эффективен по памяти, особенно для разреженных графов, где количество рёбер значительно меньше, чем количество возможных пар вершин. В случае плотных графов, где количество рёбер близко к максимальному, использование матрицы смежности может быть более удобным, но также требует больше памяти.
Пример использования списка смежности с библиотекой NetworkX:
import networkx as nx G = nx.Graph() G.add_edges_from([(1, 2), (2, 3), (3, 4)])
Для работы с большими графами важно уменьшить количество временных структур, используемых в процессе обработки. Например, избегание копирования данных на каждом шаге алгоритма, использование генераторов и итераторов вместо создания полных коллекций, помогает существенно снизить потребление памяти.
Алгоритмы обхода графа (поиск в глубину или в ширину) должны быть оптимизированы с учётом особенностей графа. Например, для поиска в глубину можно использовать рекурсию с ограничением по глубине или итеративные подходы, чтобы избежать переполнения стека при глубоком обходе.
Для ускорения вычислений при работе с большими графами можно использовать параллельные вычисления. Библиотека Dask, поддерживающая параллельное выполнение задач, может быть использована для распределённой обработки больших графов. Это позволяет значительно уменьшить время работы при наличии нескольких процессоров.
Также полезно применять алгоритмы с асимптотической эффективностью O(E) или O(V) для обхода графов. Например, алгоритм Дейкстры можно оптимизировать с помощью приоритетной очереди, что ускоряет нахождение кратчайших путей в графах с большим количеством рёбер.
Для работы с графами в Python также существует ряд библиотек, оптимизированных для больших данных. Библиотека Graph-tool, например, реализует оптимизированные алгоритмы для работы с большими графами за счёт использования C++ на уровне ядра, что позволяет существенно повысить скорость обработки данных по сравнению с чисто Python-реализациями.
Наконец, стоит обратить внимание на использование форматов хранения графов, таких как GraphML или GML. Эти форматы позволяют эффективно сериализовать графы и работать с ними на диске, что особенно полезно при работе с графами, размеры которых не помещаются в память. Загрузка и сохранение графов в эти форматы также ускоряются при использовании специализированных библиотек, таких как pyGraphML или NetworkX.
Итак, для эффективной работы с большими графами в Python важно оптимизировать как память, так и алгоритмическую сложность. Использование подходящих структур данных, библиотек и алгоритмов, а также использование параллельных вычислений и эффективных форматов хранения позволяет значительно ускорить работу с графами любого размера.
Вопрос-ответ:
Как начать строить графы в Python?
Для начала необходимо выбрать подходящую библиотеку. Одной из самых популярных является NetworkX. Для установки этой библиотеки можно использовать команду `pip install networkx`. После этого создайте пустой граф с помощью `G = nx.Graph()`, где `G` — это объект графа. Далее можно добавлять узлы с помощью `G.add_node()` и рёбра с помощью `G.add_edge()`. Этот процесс позволяет строить простые графы, к примеру, социальные сети или сети дорог.
Как визуализировать графы в Python?
Для визуализации графов в Python чаще всего используют библиотеку Matplotlib в связке с NetworkX. Важным шагом является использование функции `nx.draw()`, которая позволяет отобразить граф. Пример: после создания графа `G`, вы можете использовать команду `nx.draw(G, with_labels=True)`, чтобы увидеть граф с подписями узлов. Если нужно изменить внешний вид, можно указать дополнительные параметры, такие как цвет рёбер, форма узлов и шрифты меток.
Можно ли в Python строить графы с направленными рёбрами?
Да, для этого в NetworkX есть специальный класс для направленных графов — `DiGraph`. Чтобы создать такой граф, нужно использовать команду `G = nx.DiGraph()`. Направление рёбер можно задавать при добавлении рёбер: например, `G.add_edge(1, 2)` будет означать, что есть направленное ребро от узла 1 к узлу 2. Для визуализации направленных графов можно использовать `nx.draw_networkx_edges(G, arrows=True)` для отображения стрелок на рёбрах.
Какие ещё библиотеки для работы с графами можно использовать в Python?
Кроме NetworkX, существует несколько других библиотек, которые могут быть полезны для работы с графами в Python. Например, библиотеки Graph-tool и igraph предлагают дополнительные функциональные возможности и более высокую производительность, особенно при работе с большими графами. Graph-tool использует C++ для более быстрой работы, а igraph также поддерживает множество операций над графами и визуализацию. Выбор зависит от конкретных требований проекта, таких как размер данных и нужды в быстродействии.