Как выразить переменную из уравнения в mathcad

Mathcad предоставляет удобные инструменты для символьной и численной работы с уравнениями, включая возможность выразить переменную через другие переменные. Это особенно важно при подготовке инженерных расчётов, где необходимо быстро переопределить одну из переменных в зависимости от изменяющихся условий задачи.

Для выражения переменной используется функция solve или оператор → (если включён символьный режим). Например, при наличии уравнения F = m·a, чтобы выразить m, достаточно ввести: solve(F = m·a, m). Mathcad вернёт выражение m = F/a. Это сокращает время на алгебраические преобразования и снижает риск ошибок при ручных вычислениях.

При работе с более сложными уравнениями, содержащими тригонометрические или логарифмические функции, рекомендуется использовать консоль символических вычислений или функцию symbolic solve. Она обеспечивает более точное упрощение выражений и позволяет задавать несколько уравнений и переменных одновременно. Например: solve({x + y = 5, x — y = 1}, {x, y}).

Важно учитывать, что Mathcad чувствителен к синтаксису. Все переменные должны быть заранее определены или входить в состав уравнения. Если переменная не может быть выражена явно, Mathcad возвращает результат в неявной форме или сообщает об ошибке, что указывает на необходимость дополнительных преобразований исходного уравнения.

При необходимости получения численного значения выражённой переменной, можно использовать команду float после символьного преобразования. Это особенно полезно, когда результат необходимо использовать в дальнейшем расчёте как числовую константу.

Как выразить переменную через оператор solve

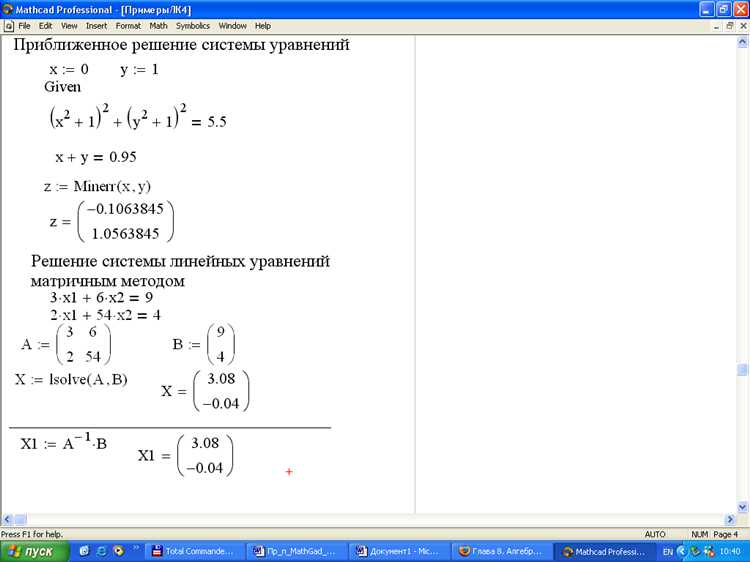
В Mathcad оператор solve используется для алгебраического решения уравнений и систем уравнений. Он применяется через встроенную функцию find совместно с ключевым словом given. Ниже описан пошаговый процесс выражения переменной.

1. Определите все входные параметры и известные значения.
2. Запишите уравнение или систему уравнений, включающую нужную переменную.
3. Перед уравнениями разместите ключевое слово given, сигнализирующее о начале условия задачи.
4. После уравнений добавьте выражение переменная := find(переменная).

Пример:

a := 5
b := 3
given
a·x + b = 0
x := find(x)

• given инициирует блок уравнений;
• find(x) запускает символьный или численный решатель;
• Результатом является значение x, удовлетворяющее уравнению.

Если уравнение нелинейное или система сложная, предварительно задайте приближённые значения переменных или используйте оператор root для явного указания интервала поиска.

given
x^3 - 2·x + 1 = 0
x := root(x^3 - 2·x + 1, x, -2, 2)

Использование функции «Given» для задания условий

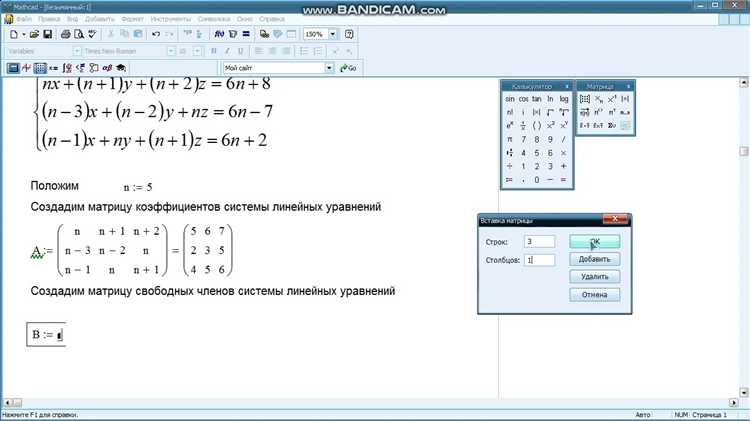
Функция Given в Mathcad необходима для постановки системы уравнений и условий, которые должны быть выполнены одновременно. Она используется в связке с функциями find или minerr для поиска значений переменных, удовлетворяющих этим условиям.

Перед вызовом find, необходимо задать все уравнения и неравенства в виде отдельных строк, а затем указать Given. Эта команда указывает Mathcad, что далее следуют определения системы условий. Пример:

x + y = 10
x - y = 4
Given
find(x, y)

Mathcad анализирует введённые до find выражения и решает систему численно. Переменные в find должны быть заранее определены в области видимости документа. Убедитесь, что количество уравнений соответствует количеству неизвестных, иначе результат будет некорректным или вызовет ошибку.

Для задания ограничений используйте знаки <, >, ≤, ≥. Пример с ограничениями:

x + y = 10
x > 0
y < 7
Given
find(x, y)

Если система не имеет точного решения, применяйте minerr вместо find, чтобы получить приближённое решение с минимальной ошибкой. Использование Given обязательно и в этом случае.

Функция Given поддерживает численные и символьные переменные, но не работает с символьными операторами решения. Она эффективна при решении задач оптимизации и систем уравнений с параметрами, когда аналитическое выражение невозможно получить напрямую.

Решение уравнения с несколькими переменными

Для решения уравнений с несколькими переменными в Mathcad применяют методы изолирования одной переменной или численные алгоритмы. При аналитическом решении следует задать уравнение в явном виде, используя оператор равенства := и выражая нужную переменную через остальные.

Если уравнение линейное и количество уравнений совпадает с числом переменных, применяется система уравнений с функцией solve или linsolve. Для одного уравнения с несколькими неизвестными задается фиксированное значение всех переменных, кроме искомой, и производится выражение переменной с помощью функции solve или через операторы Mathcad.

В случае нелинейных уравнений используют численные методы, например, функция root, с указанием начального приближения для каждой переменной. Начальные значения влияют на сходимость и корректность результата, поэтому их следует выбирать исходя из анализа уравнения или графика.

При необходимости получить выражение переменной в явном виде без численных методов рекомендуется использовать встроенный оператор solve для символьного преобразования, но его применение ограничено сложностью уравнения и возможностями встроенного движка Mathcad.

Работа с системой уравнений в контексте выражения переменной

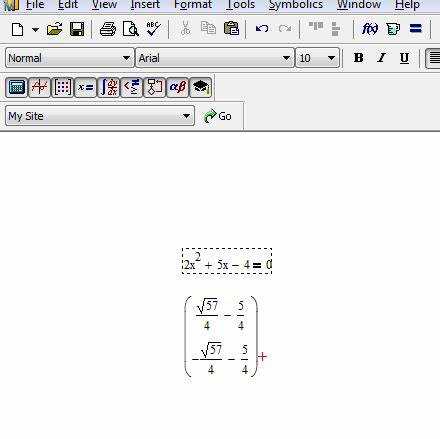
Последовательность действий включает формулировку системы уравнений в виде набора выражений с использованием оператора «=». Затем задаётся переменная или вектор переменных, которые нужно найти, после чего применяется функция решения. В случае выражения конкретной переменной из системы она задаётся как искомая, а остальные – как параметры или известные величины.

Для упрощения решения рекомендуется предварительно упростить уравнения, исключив избыточные или линейно зависимые уравнения, что повысит устойчивость вычислений. Mathcad автоматически формирует матричные представления системы и применяет методы, основанные на обратных матрицах или методах Ньютона для нелинейных систем.

Если система не может быть решена аналитически, Mathcad возвращает численное приближение. В таких случаях важно задавать начальные приближения для переменных, используя оператор «Guess». Это существенно ускоряет сходимость и снижает вероятность ошибок.

При выражении переменной из системы уравнений важно контролировать размерность и типы переменных. Mathcad требует чёткой идентификации скалярных или векторных переменных, что влияет на результат вычислений и корректность формул.

Для автоматизации часто используют выражения, связывающие найденные переменные с последующими вычислениями, что позволяет динамически изменять параметры системы и мгновенно получать обновлённые значения искомых переменных.

Выражение переменной в символическом решении

В Mathcad для получения выражения переменной из уравнения применяется встроенный символический движок. Он позволяет вывести аналитическую форму переменной без численных приближений.

1. Для начала введите уравнение в виде, например, eq := a*x + b = 0.
2. Используйте функцию solve(eq, x) для получения символического решения относительно переменной x.
3. Если уравнение имеет несколько корней, результатом будет набор выражений, каждый из которых можно извлечь с помощью индексации, например, solve(eq, x)[0].
4. Для упрощения результата используйте функцию simplify(), которая уменьшает сложность выражения, устраняя избыточные части.
5. В случае систем уравнений применяйте solve(system, vars), где vars – вектор переменных для выражения.
6. Обратите внимание: символический движок ограничен по степени уравнений и сложности выражений. При невозможности получить аналитическое решение Mathcad вернёт пустой результат.

Рекомендуется:

• Чётко задавать переменную, которую необходимо выразить, чтобы избежать неоднозначности.
• Перед символическим решением проверить уравнение на корректность и совместимость.
• Использовать функции expand() и factor() для дальнейшей работы с выражением.

Ошибки при попытке выразить переменную и способы их устранения

При выражении переменной из уравнения в Mathcad часто возникают ошибки, связанные с синтаксисом, структурой уравнения и спецификой используемых функций. Основные проблемы и их решения представлены ниже.

1. Неправильное использование знака равенства

В Mathcad для определения переменной используется знак равенства “:=”, а не “=”. Попытка выразить переменную через обычное “=” приводит к ошибке или неверному результату. Решение: использовать оператор присваивания “:=” для задания выражения переменной.

2. Несоответствие количества переменных и уравнений

Mathcad не может однозначно выразить переменную, если система уравнений недостаточно определена. Если переменная участвует в нескольких уравнениях, необходимо либо дополнительно задать условия, либо использовать функцию решения систем, например, solve(). Решение: проверять, что число уравнений соответствует числу переменных и применять solve() для систем.

3. Ошибки в синтаксисе выражений

Отсутствие скобок, неправильное использование операторов или функций приводит к синтаксическим ошибкам. Mathcad требует строго соблюдать порядок операций и явное группирование. Решение: всегда использовать скобки для сложных выражений и проверять корректность вложенности.

4. Попытка выражения переменной из неалгебраического уравнения

Если уравнение содержит интегралы, производные или логарифмы, Mathcad не всегда может аналитически решить его для переменной. В таких случаях необходимо использовать численные методы solve или optimize. Решение: переключаться на численные методы и задавать начальные приближения.

5. Несоответствие типа переменной и функции

Mathcad требует, чтобы переменные имели соответствующий тип данных (число, вектор, матрица). Попытка выразить скаляр через векторное уравнение без приведения типов вызывает ошибку. Решение: применять функции преобразования типов или корректно задавать размерность переменных.

6. Использование зарезервированных имен

Попытка выразить переменную с именем, совпадающим с функцией Mathcad, приводит к конфликтам. Решение: выбирать уникальные имена переменных, избегая стандартных функций и констант.

7. Ошибки при использовании solve()

Функция solve требует правильной постановки уравнения с использованием оператора “=”, а не “:=”, внутри её аргументов. Часто ошибка возникает, если смешать операторы или задать уравнение неверно. Решение: для solve использовать строго равенство, правильно формулировать условие и проверять результат на пустой или множественный набор решений.

Особенности выражения переменных при работе с матрицами

В Mathcad переменные, заданные как матрицы, требуют точного указания индексов для извлечения элементов или подматриц. Использование конструкции вида A[i,j] возвращает элемент в i-й строке и j-м столбце. При выражении переменной важно учитывать порядок индексов – сначала строка, затем столбец.

Если переменная задаётся как матрица, попытка присвоить значение без индексации приводит к переопределению всей матрицы, а не отдельного элемента. Для изменения одного элемента следует использовать отдельное выражение с индексами, например, A[2,3] := 5.

Mathcad поддерживает векторизацию операций с матрицами. При выражении переменных рекомендуется применять встроенные функции с матричной арифметикой, избегая поэлементного цикла там, где это возможно. Это ускоряет вычисления и сохраняет структуру данных.

При работе с подматрицами переменная может выражаться через диапазон индексов, например, A[1..3,2..4] – это срез матрицы с первой по третью строку и со второго по четвёртый столбец. Важно помнить, что при таком выражении создаётся новая матрица, а не ссылка на оригинал, следовательно, изменение её элементов не повлияет на исходную матрицу.

Mathcad не поддерживает динамическое изменение размера матрицы через выражение переменной. Для добавления строк или столбцов следует использовать функции объединения или создавать новую матрицу с нужными размерами.

При выражении переменных в формулах с матрицами необходимо учитывать тип данных – числовой или символический. Для числовых матриц Mathcad автоматически оптимизирует вычисления, тогда как символические выражения требуют явного определения элементов и операций, иначе возможна потеря точности или увеличение времени обработки.

Вопрос-ответ:

Как в Mathcad можно выразить переменную из уравнения?

В Mathcad для выражения переменной из уравнения обычно используют функцию решения уравнений. Можно записать уравнение с неизвестной переменной и применить оператор «solve» или воспользоваться встроенным инструментом для нахождения корней. Результат будет отображать значение искомой переменной.

Какие особенности работы с нелинейными уравнениями при выражении переменной в Mathcad?

При работе с нелинейными уравнениями Mathcad применяет численные методы, поэтому результат зависит от начального приближения. Для точного вычисления нужно задать подходящее начальное значение, иначе решение может не быть найдено или будет неверным. Также в таких случаях часто требуется анализировать поведение функции и выбирать корректные параметры.

Можно ли получить аналитическое выражение переменной из уравнения в Mathcad?

Mathcad позволяет получить аналитическое выражение переменной, но только в случаях, когда уравнение имеет стандартное или простое решение. Для сложных уравнений чаще применяется численный метод. Если уравнение решаемо аналитически, Mathcad покажет формулу, иначе выдаст численное значение.

Как в Mathcad задать несколько уравнений для одновременного выражения нескольких переменных?

Для решения системы уравнений в Mathcad необходимо ввести все уравнения вместе с переменными и использовать функцию решения систем. Mathcad позволяет указать список переменных, которые нужно найти, и выдаст значения или выражения для каждой из них, при условии, что система имеет решение.

Какие ошибки могут возникнуть при попытке выразить переменную из уравнения в Mathcad и как их избежать?

Основные ошибки связаны с неправильным вводом уравнений, отсутствием заданных значений для параметров или выбором неподходящего метода решения. Чтобы избежать проблем, нужно внимательно проверять синтаксис, использовать корректные обозначения, а также задавать начальные приближения для численных методов, если это необходимо.

Как в Mathcad можно выразить одну переменную через другую из заданного уравнения?

В Mathcad для выражения одной переменной через другую из уравнения обычно используют функции решения уравнений, такие как solve или root. Сначала задаётся исходное уравнение с переменными, после чего выбирается переменная, которую требуется найти. Затем применяется соответствующая команда, позволяющая получить формулу или численное значение искомой переменной в зависимости от заданных значений других параметров.