Как работает рекурсия в python

Рекурсия в Python – это вызов функции самой себя с новыми аргументами. Она применяется, когда задачу можно разбить на подзадачи того же типа. Классический пример – вычисление факториала: n! = n × (n — 1)!. В языке Python рекурсия реализуется через обычные функции, но существует ограничение по глубине вложенности – по умолчанию 1000 вызовов. Его можно изменить через sys.setrecursionlimit(), но делать это стоит с осторожностью из-за риска переполнения стека.

Для практического понимания важно рассмотреть не только математические примеры, но и задачи на обход структур данных. Например, обход дерева или графа часто реализуется рекурсивно. При этом важно контролировать условия выхода из рекурсии, иначе возникает RecursionError. В задачах на парсинг вложенных структур (например, JSON) или обход файловой системы рекурсия позволяет выразить алгоритм лаконично и без явной очереди или стека.

Рекурсивные функции в Python создают новую область видимости при каждом вызове. Это значит, что все локальные переменные не сохраняются между вызовами. Чтобы передавать состояние, используют аргументы функции. Также важно избегать повторных вычислений при пересечении ветвей рекурсии. Для этого применяют мемоизацию – вручную через словарь или с помощью @lru_cache из модуля functools.

На практике рекурсия часто проигрывает итерации по производительности. Например, задача вычисления чисел Фибоначчи рекурсивно без кеша имеет экспоненциальную сложность. Поэтому рекурсию применяют там, где логика задачи требует вложенного вызова, а не везде, где это возможно технически. Важно понимать, как будет разворачиваться стек вызовов и где именно функция завершает выполнение.

Как работает стек вызовов при рекурсивных функциях

При вызове рекурсивной функции Python сохраняет контекст каждого вызова в стеке. Контекст включает значения аргументов, адрес возврата и локальные переменные. Каждый новый вызов помещает кадр (frame) в стек. При достижении базового случая функция начинает возвращать значения, и кадры снимаются с вершины стека в обратном порядке.

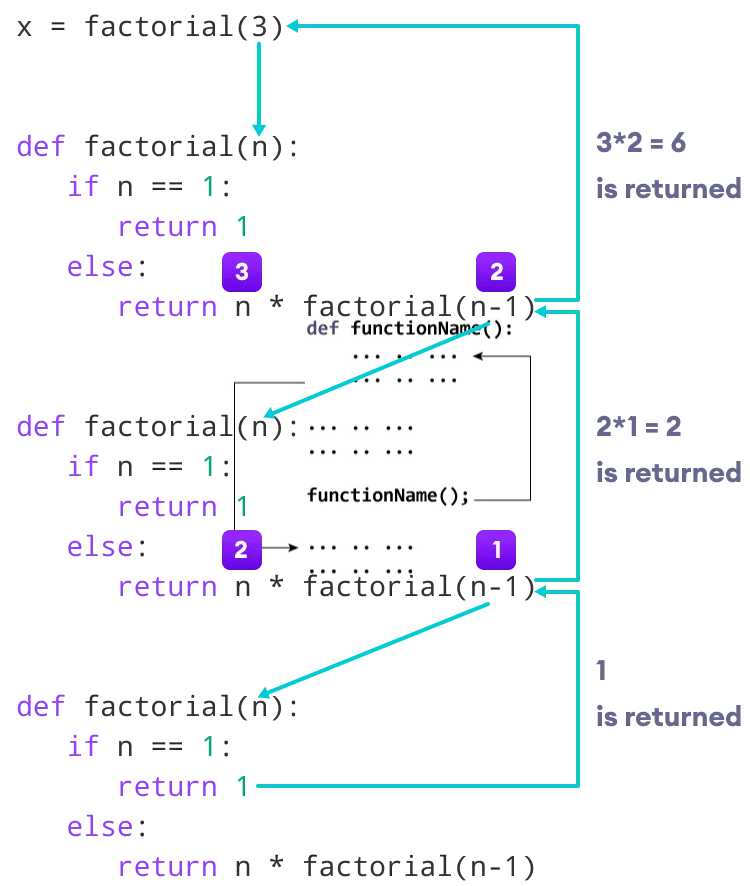
Рассмотрим функцию вычисления факториала:

def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)

Вызов factorial(3) создаёт стек из четырёх кадров: factorial(3), factorial(2), factorial(1), factorial(0). После достижения n == 0 начинается разворачивание: factorial(0) возвращает 1, затем каждый кадр перемножает результат и передаёт его вверх.

Если глубина рекурсии превышает значение sys.getrecursionlimit() (по умолчанию 1000), возникает RecursionError. Для контроля глубины можно использовать sys.setrecursionlimit(), но при этом увеличивается риск переполнения стека ОС. Вместо этого лучше применять хвостовую рекурсию или итеративные решения.

Диагностику поведения стека упрощает модуль traceback. Для отслеживания глубины полезна отладка через pdb или логирование аргументов на входе функции.

Стек вызовов в CPython реализован через C-стек, поэтому важно учитывать ограничения платформы. При проектировании рекурсивных алгоритмов необходимо контролировать количество вызовов и обеспечивать достижение базового случая в каждом возможном пути выполнения.

Где и как возникает переполнение стека в Python

Переполнение стека (StackOverflow) в Python возникает при превышении лимита глубины рекурсии, установленного интерпретатором. По умолчанию этот предел составляет 1000 вызовов. Его можно получить и изменить с помощью модуля sys:

import sys
print(sys.getrecursionlimit())  # обычно 1000
sys.setrecursionlimit(1500)     # изменение лимита

Ошибка проявляется как RecursionError: maximum recursion depth exceeded. Она не зависит от сложности алгоритма, а исключительно от глубины вложенных вызовов функций.

Неформальные структуры данных, как например дерево или граф, часто приводят к глубоким вызовам, особенно при DFS (обход в глубину) без отслеживания посещённых узлов.
Ошибки в базовом случае рекурсивной функции (например, неправильная или отсутствующая проверка выхода) приводят к бесконечной рекурсии.
Даже при корректной логике рекурсивные алгоритмы, такие как вычисление чисел Фибоначчи без мемоизации, быстро достигают лимита:

def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
fib(997)  # ещё работает
fib(998)  # RecursionError

Чтобы избежать переполнения:

Используйте итеративные алгоритмы вместо рекурсивных при линейной структуре данных.
Для деревьев и графов используйте явный стек (например, список) вместо системного.
Контролируйте глубину и условия выхода из рекурсии.
Используйте декораторы lru_cache или ручную мемоизацию для устранения повторных вызовов.
Не увеличивайте лимит sys.setrecursionlimit() без крайней необходимости – это может привести к сбою интерпретатора или ОС.

Разница между прямой и хвостовой рекурсией на примерах

def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)

Каждый вызов функции сохраняется в стеке до момента достижения базового случая. После этого начинается обратный проход, при котором происходит перемножение всех значений. При больших n стек вызовов быстро заполняется, что приводит к RecursionError.

Хвостовая рекурсия предполагает, что рекурсивный вызов является последней операцией в функции. Это позволяет оптимизировать использование стека при наличии соответствующей поддержки в интерпретаторе. Пример:

def tail_factorial(n, acc=1):
if n == 0:
return acc
return tail_factorial(n - 1, acc * n)

Здесь переменная acc аккумулирует результат, избавляя от необходимости возвращаться к предыдущим кадрам стека. Однако Python не оптимизирует хвостовую рекурсию, и с точки зрения использования памяти этот подход не даёт преимущества. Тем не менее, такая форма удобна для преобразования в итеративный алгоритм:

def iter_factorial(n):
acc = 1
while n > 0:
acc *= n
n -= 1
return acc

Итеративная реализация выполняется быстрее и не требует стековой памяти. Рекомендуется использовать хвостовой стиль для упрощения перехода от рекурсии к итерации в критичных по производительности задачах.

Когда использовать рекурсию вместо цикла: практические сценарии

Рекурсия полезна в тех случаях, когда задача может быть разбита на несколько схожих подзадач, каждая из которых имеет однотипную структуру. Это часто встречается в задачах с деревьями, графами и разделением задачи на более мелкие подзадачи. Рассмотрим несколько случаев, когда рекурсия более эффективна или понятна, чем цикл.

1. Работа с деревьями: Когда необходимо обходить структуры данных типа дерева или графа, рекурсия позволяет удобно и лаконично решать задачу. Например, обход бинарного дерева или поиск в глубину в графах часто требует минимального кода при использовании рекурсии. В цикле такой обход потребует более сложной логики для работы с состоянием и стеком.

2. Алгоритмы с динамическим делением задачи: Задачи типа «разделяй и властвуй», например сортировка слиянием или быстрая сортировка, естественно выражаются через рекурсию. Здесь проблема делится на подзадачи, которые решаются рекурсивно, что упрощает код и уменьшает вероятность ошибок. В цикле такой подход был бы не таким очевидным и требовал бы дополнительного управления состоянием.

3. Упрощение кода для рекурсивных структур: Если задача требует обращения к элементам, которые организованы в рекурсивные структуры, например, при анализе выражений или вычислении факториала, рекурсия помогает избежать сложной логики с ручным управлением состоянием, которое обычно требуется при использовании циклов.

4. Решение задач с неопределённым числом итераций: В случаях, когда количество итераций заранее неизвестно, например, при вычислении чисел Фибоначчи или в задаче о ханойских башнях, рекурсия позволяет естественно и гибко решать проблему, без необходимости заранее определять пределы цикла.

5. Логические задачи: Для задач, в которых необходимо отслеживать несколько состояний или ветвей возможных решений, рекурсия предоставляет чистое и понятное решение. Например, в задаче о поиске всех путей в лабиринте или решении головоломок с несколькими путями, рекурсия позволяет красиво моделировать все варианты.

6. Генерация сочетаний и перестановок: Рекурсия является наиболее удобным инструментом для решения задач, связанных с генерацией всех возможных вариантов, таких как перебор всех подмножеств множества или генерация перестановок. Циклические решения требуют дополнительной логики и могут быть менее читабельными.

Использование рекурсии вместо цикла оправдано, когда структура задачи естественно поддаётся разделению на подзадачи, и рекурсивное решение делает код более понятным и кратким. Важно помнить, что рекурсия требует большего потребления памяти из-за работы стека вызовов, что может стать проблемой при глубокой рекурсии. В таких случаях необходимо учитывать это ограничение и по возможности оптимизировать решение, например, применяя хвостовую рекурсию или итерационные подходы.

Оптимизация рекурсивных алгоритмов с помощью кеширования

Кеширование (или мемоизация) – это техника сохранения результатов предыдущих вычислений, чтобы избежать их повторного выполнения. В Python для этого можно использовать встроенный декоратор @functools.lru_cache, который автоматически кеширует результаты функции. Это значительно ускоряет рекурсивные алгоритмы, минимизируя количество вызовов с одинаковыми параметрами.

Рассмотрим пример использования мемоизации на примере вычисления чисел Фибоначчи:

import functools
@functools.lru_cache(maxsize=None)  # Неограниченный кеш
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)

В данном примере декоратор @functools.lru_cache сохраняет результаты вычислений для каждого числа Фибоначчи, что позволяет избежать многократных вычислений одних и тех же значений. В результате, если функция fibonacci(n) вызывается несколько раз с одинаковыми аргументами, Python просто вернёт значение из кеша, что ускоряет выполнение программы.

Преимущества использования кеширования:

Снижение количества повторных вычислений.
Ускорение работы программы, особенно при больших входных данных.
Уменьшение нагрузки на память, так как результаты сохраняются на уровне функции.

Тем не менее, важно учитывать несколько факторов при применении кеширования:

Не все задачи требуют кеширования. Если рекурсия затрагивает небольшие данные или количество уникальных вызовов невелико, кеширование не даст значительного прироста в производительности.
При использовании кеша необходимо следить за его размером. При больших данных может возникнуть переполнение памяти, особенно если кеш хранит данные, которые редко используются.

Для задач с ограниченными вычислениями можно ограничить размер кеша, установив параметр maxsize в functools.lru_cache. Например, установив maxsize=128, можно кешировать только последние 128 результатов.

Использование кеширования помогает значительно повысить производительность рекурсивных алгоритмов, устраняя дублирование вычислений, что особенно важно при решении сложных задач, таких как вычисление чисел Фибоначчи или решение задач на динамическое программирование.

Рекурсивные функции в задачах на обход деревьев

Рекурсивные функции активно применяются для решения задач на обход деревьев, таких как поиск, подсчёт элементов, или модификация структуры. В таких задачах дерево представляется как структура данных с узлами, которые могут содержать данные и ссылки на дочерние узлы. Рекурсия позволяет эффективно обходить дерево, применяя одну и ту же логику для текущего узла и его потомков.

Примером задачи является обход дерева в глубину (DFS). При этом для каждого узла дерева рекурсивно вызывается функция для всех дочерних узлов, начиная с корня. В Python это часто реализуется через функцию, которая принимает узел как аргумент, выполняет действия с ним, а затем вызывает себя для каждого дочернего узла.

Пример функции для обхода дерева в глубину:


class Node:
def __init__(self, value):
self.value = value
self.children = []
def depth_first_traversal(node):
print(node.value)  # Действие с текущим узлом
for child in node.children:
depth_first_traversal(child)  # Рекурсивный вызов для каждого дочернего узла

При таком подходе каждый узел обрабатывается только один раз, и рекурсия автоматически возвращает управление в точку, где завершен обход дочернего узла, продолжая с родительского узла.

Деревья могут быть разной структуры, включая бинарные деревья, где каждый узел имеет не более двух дочерних узлов. В этом случае рекурсивная функция становится проще, так как для каждого узла достаточно вызвать функцию для двух дочерних узлов (если они существуют). Пример для бинарного дерева:


class BinaryTreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def depth_first_traversal(node):
if node:
print(node.value)
depth_first_traversal(node.left)  # Обход левого поддерева
depth_first_traversal(node.right)  # Обход правого поддерева

Рекурсивные функции могут также использоваться для других видов обхода деревьев, таких как обход в ширину, где для каждой очереди узлов выполняются последовательные действия. Однако рекурсия в таких задачах чаще используется в деревьях с небольшими глубинами или в случаях, когда дерево имеет неравномерную структуру.

Основное преимущество рекурсии в таких задачах заключается в её простоте и выразительности. Вместо того чтобы вручную управлять стеком или очередью, рекурсивный вызов позволяет Python эффективно использовать стек вызовов, обеспечивая удобное и чистое решение. Тем не менее, для деревьев с очень глубокой вложенностью стоит учитывать возможные ограничения на глубину рекурсии, установленные в Python, чтобы избежать ошибок переполнения стека.

Рекурсия в задачах на разбор вложенных структур

Рекурсия часто применяется для обработки вложенных данных, таких как деревья, графы, или JSON-объекты. Рассмотрим, как она может быть использована для разборки таких структур.

Типичная задача на разбор вложенных структур – это обход и извлечение данных из вложенных списков, словарей или смешанных объектов. Рекурсия позволяет легко обработать структуры произвольной глубины, так как она природно подходит для таких задач, где структура повторяется на разных уровнях.

Пример: допустим, у нас есть сложная структура данных в виде вложенных списков. Задача – подсчитать количество элементов всех уровней вложенности. Чтобы решить эту задачу, можно использовать рекурсивную функцию, которая будет проверять каждый элемент и, если он является списком, углубляться в него.

def count_elements(data):
count = 0
for item in data:
if isinstance(item, list):
count += count_elements(item)  # рекурсивный вызов для вложенного списка
else:
count += 1  # элемент на текущем уровне
return count

В этом примере функция count_elements вызывает саму себя для каждого вложенного списка. Каждый раз, когда она встречает новый уровень вложенности, рекурсивный вызов позволяет обработать его, а возвращаемое значение суммируется для получения общего результата.

Рекурсия идеально подходит для таких задач, поскольку позволяет избежать сложных циклов и явной обработки всех уровней вложенности. Главное правило – всегда предусматривать условие выхода из рекурсии. В этом случае условием выхода является достижение простого элемента (не списка).

Другим примером может быть задача разборки JSON-объекта. Рассмотрим задачу, в которой необходимо получить все значения по ключу "name" в глубоко вложенном JSON-объекте.

def find_names(data):
names = []
if isinstance(data, dict):
for key, value in data.items():
if key == "name":
names.append(value)
elif isinstance(value, (dict, list)):
names.extend(find_names(value))  # рекурсивный вызов для вложенных объектов
elif isinstance(data, list):
for item in data:
names.extend(find_names(item))  # рекурсивный вызов для элементов списка
return names

Здесь функция find_names проходит по всем уровням структуры данных, независимо от того, являются ли элементы словарями или списками. Каждый раз, когда она встречает ключ "name", она добавляет его значение в результат.

Рекурсия позволяет строить решения для сложных структур, сводя логику к простому повторению действий на каждом уровне вложенности. Однако важно помнить, что рекурсивные решения требуют контроля за глубиной рекурсии, особенно при работе с большими или глубоко вложенными структурами. Для этого можно использовать ограничение на количество рекурсивных вызовов или преобразовать решение в итеративную форму, если это необходимо.

Отладка рекурсивного кода: пошаговый разбор

1. Визуализация стека вызовов

def factorial(n):
print(f"factorial({n})")
if n == 0:
return 1
return n * factorial(n-1)

Такой подход поможет проследить, как функция глубоко заходит в рекурсию и когда начинается выход из неё.

2. Использование отладчика

Инструменты отладки, такие как pdb, позволяют пошагово выполнять код и проверять состояние переменных на каждом уровне рекурсии. Устанавливая точку останова внутри рекурсивной функции, можно исследовать значения на каждом шаге и убедиться, что рекурсия не заходит в бесконечный цикл.

import pdb
def factorial(n):
pdb.set_trace()  # Ожидает команду отладки
if n == 0:
return 1
return n * factorial(n-1)

Использование команд n (next), s (step) и p (print) позволяет детально исследовать выполнение программы на каждом шаге.

3. Проверка базовых случаев

Базовые случаи – это место, где рекурсия должна завершиться. Проблемы часто возникают, если базовый случай неправильно реализован. Например, если базовый случай не захватывает все возможные значения или если условие выхода отсутствует. Нужно внимательно проверять, что базовый случай корректно обрабатывает все возможные входные данные.

def fibonacci(n):
if n <= 1:  # Базовый случай
return n
return fibonacci(n-1) + fibonacci(n-2)

Важно убедиться, что базовый случай охватывает все необходимые значения (например, отрицательные числа в некоторых задачах).

4. Избежание переполнения стека

Рекурсивный алгоритм может привести к переполнению стека, если глубина рекурсии слишком велика. Это особенно актуально для задач с большими входными данными. Чтобы избежать переполнения стека, можно использовать хвостовую рекурсию, где последний шаг функции вызывает саму себя.

def factorial_tail(n, acc=1):
if n == 0:
return acc
return factorial_tail(n-1, n*acc)

Если Python поддерживает хвостовую рекурсию (хотя она и не оптимизирована в стандартной реализации), такая техника помогает избежать переполнения стека, так как не добавляется новый кадр в стек вызовов.

5. Применение итерации вместо рекурсии

В некоторых случаях можно заменить рекурсию на итерацию, если задача может быть решена с помощью цикла. Это поможет избежать переполнения стека и улучшить производительность.

def factorial_iter(n):
result = 1
for i in range(1, n+1):
result *= i
return result

Преобразование рекурсии в итерацию помогает снизить нагрузку на систему, особенно при обработке больших объемов данных.

Вопрос-ответ:

Как рекурсия работает в Python и в чем её преимущества?

Рекурсия — это техника программирования, при которой функция вызывает сама себя. В Python рекурсия используется, когда задача может быть решена путём деления на более простые подзадачи. Например, при решении задач, таких как нахождение факториала или обход файловой системы. Преимущества рекурсии заключаются в том, что она позволяет решать задачи более элегантно, сокращая количество кода и улучшая его читаемость. Однако стоит помнить, что чрезмерное использование рекурсии может привести к проблемам с памятью, так как каждый вызов функции требует выделения нового пространства на стеке вызовов.

Почему важно учитывать ограничения по глубине рекурсии в Python?

В Python существует ограничение на глубину рекурсии, которое по умолчанию составляет 1000. Это сделано для того, чтобы избежать переполнения стека вызовов, что может привести к ошибке `RecursionError`. Если рекурсия будет слишком глубокой, память, выделенная для хранения каждого вызова функции, будет исчерпана. Это может произойти, если, например, ошибка в логике программы приводит к бесконечным рекурсивным вызовам. Чтобы избежать этой проблемы, важно проверять условие выхода из рекурсии или увеличивать предел рекурсии с помощью модуля `sys`, но с осторожностью.

Как избежать переполнения стека при использовании рекурсии?

Чтобы избежать переполнения стека при рекурсии, необходимо учитывать два момента. Во-первых, важно правильно определить базовый случай — условие, при котором рекурсивная функция перестаёт вызывать себя. Во-вторых, можно использовать так называемую "хвостовую рекурсию", когда результат рекурсивного вызова возвращается сразу же, не создавая новых фреймов стека. В Python нет оптимизации хвостовой рекурсии, как в некоторых других языках, но это всё равно полезный подход, который помогает минимизировать использование памяти. Альтернативой рекурсии может быть использование итераций, что предотвращает переполнение стека.

Какие реальные примеры использования рекурсии можно найти в Python?

Рекурсия широко используется в решении задач, связанных с делением на подзадачи. Примером может быть нахождение факториала числа, где каждый следующий шаг сводится к вычислению меньшего факториала. Также рекурсия применяется при работе с деревьями и графами, например, для поиска в глубину в графах или обхода файловой системы. Ещё один пример — решение задачи о нахождении чисел Фибоначчи, где каждое число зависит от предыдущих двух. Рекурсия также используется в алгоритмах сортировки, таких как "быстрая сортировка" или "сортировка слиянием". Такие задачи хорошо решаются через рекурсию благодаря её способности справляться с множеством одинаковых подзадач.