Как считается сумма чисел фибоначчи python

Числа Фибоначчи составляют одну из самых известных числовых последовательностей, которая начинается с 0 и 1, а каждое следующее число является суммой двух предыдущих. В программировании эта последовательность используется для решения различных задач, таких как динамическое программирование, обработка данных и генерация числовых последовательностей. Одной из распространенных задач является вычисление суммы первых N чисел Фибоначчи.

На Python существует несколько способов решения этой задачи. Использование рекурсии и итерации – два самых популярных подхода. Рекурсия легко понимается и интуитивно привлекает внимание, однако для больших значений N она может быть неэффективной из-за большого количества повторяющихся вычислений. Итерационный метод, с другой стороны, может быть значительно быстрее и менее затратным по памяти.

Кроме того, Python предоставляет богатые встроенные функции для работы с последовательностями, что позволяет создавать эффективные решения. Одним из таких решений является использование генераторов и оптимизации с помощью мемоизации. В этом примере рассмотрим как можно вычислить сумму чисел Фибоначчи для заданного числа N с использованием эффективного итеративного подхода.

Создание функции для вычисления чисел Фибоначчи с использованием цикла

Числа Фибоначчи представляют собой последовательность, в которой каждое число равно сумме двух предыдущих. Важно понимать, что с помощью цикла можно эффективно вычислять значения чисел Фибоначчи, избегая рекурсивных вызовов, которые могут привести к значительному снижению производительности.

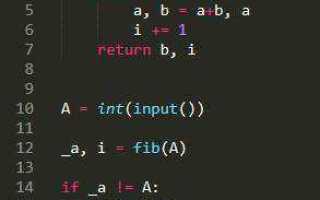
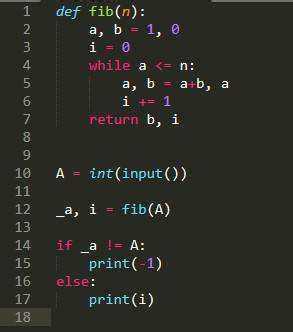
Функция для вычисления чисел Фибоначчи с использованием цикла значительно проще по сравнению с рекурсивным методом. Рассмотрим создание такой функции для нахождения n-го числа Фибоначчи:

pythonEditdef fibonacci(n):

if n <= 0:

return «Число должно быть положительным»

elif n == 1:

return 0

elif n == 2:

return 1

a, b = 0, 1

for _ in range(2, n):

a, b = b, a + b

return b

В данной функции сначала проверяются крайние случаи (если число меньше или равно нулю), затем для первых двух чисел Фибоначчи возвращаются значения 0 и 1. После этого с помощью цикла считаются все последующие числа. Переменные a и b хранят два последних числа последовательности, и на каждом шаге они обновляются.

Преимущества использования цикла:

• Меньше накладных расходов на память по сравнению с рекурсией.
• Быстрее при вычислении больших чисел, так как цикл работает за время O(n).
• Простота реализации и минимизация риска переполнения стека при больших значениях n.

Функция fibonacci(n) возвращает n-е число Фибоначчи, где n – это целое положительное число. Этот подход позволяет обрабатывать достаточно большие значения n без потери производительности.

Реализация рекурсивной функции для вычисления чисел Фибоначчи

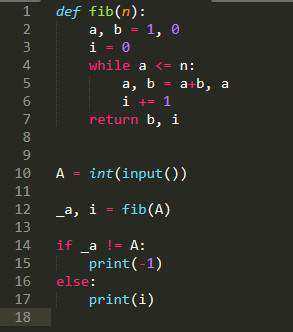
Пример реализации рекурсивной функции на Python:

def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)

В этой реализации:

• Базовые случаи: если n = 0, возвращаем 0, если n = 1, возвращаем 1.
• В противном случае, функция вызывает себя для двух меньших значений n, что соответствует рекурсивному определению чисел Фибоначчи.

Преимущества и недостатки рекурсивного метода:

• Легкость понимания алгоритма, так как он напрямую соответствует определению последовательности Фибоначчи.
• Рекурсивный подход может быть неэффективным для больших значений n из-за повторных вычислений одних и тех же значений. Например, для n = 50 рекурсивный метод будет выполнять экспоненциальное количество вызовов.

Чтобы улучшить эффективность, можно использовать метод мемоизации. Это сохранение результатов рекурсивных вызовов в кэше, что позволяет избежать многократных вычислений одинаковых значений.

Пример с мемоизацией:

def fibonacci_memo(n, memo={0: 0, 1: 1}):
if n not in memo:
memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
return memo[n]

В этой версии:

• Мемоизация значительно ускоряет работу, так как каждый результат сохраняется и используется повторно при необходимости.
• Алгоритм работает за время O(n), что значительно быстрее рекурсивного метода без мемоизации (O(2^n)).

Рекурсивный способ подходит для небольших значений n и учебных целей, однако для больших вычислений рекомендуется использовать итеративные методы или мемоизацию для повышения эффективности.

Использование метода динамического программирования для вычисления суммы

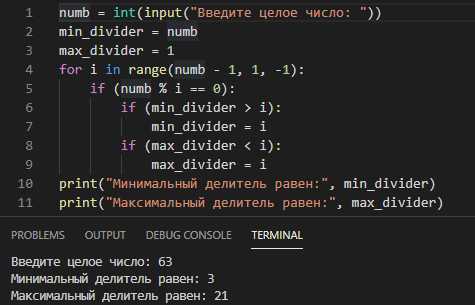
Для вычисления суммы первых N чисел Фибоначчи можно использовать подход, при котором значения чисел Фибоначчи сохраняются в массиве, чтобы избежать повторных вычислений. Это позволяет существенно улучшить производительность, особенно для больших значений N.

Алгоритм с использованием динамического программирования включает следующие шаги:

1. Инициализация массива для хранения чисел Фибоначчи.
2. Заполнение массива с использованием формулы: F(n) = F(n-1) + F(n-2), где F(0) = 0 и F(1) = 1.
3. Вычисление суммы элементов массива.

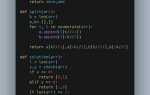
Пример кода для вычисления суммы первых N чисел Фибоначчи:

def sum_fibonacci(n):
if n <= 0:
return 0
elif n == 1:
return 1
fib = [0] * (n+1)
fib[1] = 1
total_sum = fib[0] + fib[1]
for i in range(2, n+1):
fib[i] = fib[i-1] + fib[i-2]
total_sum += fib[i]
return total_sum

В этом коде мы создаем массив fib, где каждый элемент хранит значение соответствующего числа Фибоначчи. После вычисления всех чисел мы суммируем их, начиная с индексов 0 и 1. Время работы этого алгоритма – O(N), что значительно быстрее, чем рекурсивное вычисление.

Для еще большего ускорения можно использовать два вспомогательных переменных вместо всего массива, поскольку для вычисления текущего числа Фибоначчи достаточно только двух предыдущих. Это уменьшает потребление памяти до O(1).

def sum_fibonacci_optimized(n):
if n <= 0:
return 0
elif n == 1:
return 1
a, b = 0, 1
total_sum = a + b
for _ in range(2, n+1):
a, b = b, a + b
total_sum += b
return total_sum

Этот вариант также работает за O(N), но использует только два числа для хранения промежуточных значений. Такой подход более эффективен по памяти.

Использование динамического программирования позволяет значительно сократить время выполнения программы, особенно при большом значении N. Это делает метод идеальным для вычислений, требующих высокой производительности и малых затрат памяти.

Как вычислить сумму чисел Фибоначчи с ограничением по числу членов

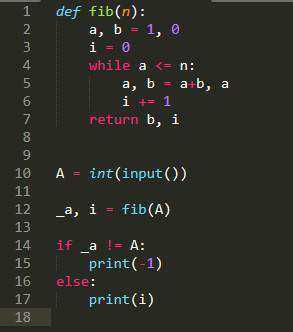
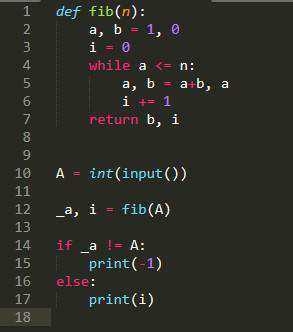
Для вычисления суммы чисел Фибоначчи с ограничением по числу членов, можно использовать несколько подходов, включая рекурсию и итерацию. Однако итеративный метод предпочтительнее по производительности, особенно при большом числе членов. Рассмотрим решение задачи с использованием цикла.

Последовательность Фибоначчи начинается с чисел 0 и 1, и каждое последующее число является суммой двух предыдущих. Например, первые 10 чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.

Для того чтобы найти сумму чисел Фибоначчи, ограниченную числом членов, нужно пройти по последовательности до заданного количества чисел и вычислить их сумму.

Пример кода для вычисления суммы первых N чисел Фибоначчи:

def sum_fibonacci(n):
a, b = 0, 1
total = 0
for _ in range(n):
total += a
a, b = b, a + b
return total

В этом примере функция sum_fibonacci(n) принимает параметр n – количество чисел Фибоначчи, которые нужно суммировать. Внутри функции используются переменные a и b для хранения текущих чисел Фибоначчи, а переменная total для накопления суммы. В цикле происходит добавление текущего числа Фибоначчи в сумму и обновление значений чисел для следующего шага.

Такой подход обладает временем работы O(n), что делает его эффективным даже для больших значений n.

Для меньших значений чисел, можно легко использовать рекурсию, но этот метод имеет большую сложность из-за повторных вычислений. Поэтому для больших значений предпочтительнее использовать итеративные методы или динамическое программирование.

Использование генераторов для оптимизации вычислений чисел Фибоначчи

Генераторы в Python позволяют значительно оптимизировать вычисления чисел Фибоначчи благодаря своей способности работать с последовательностями без необходимости хранить все элементы в памяти. Это особенно важно при больших значениях чисел, когда вычисления могут занять значительное время и ресурсы.

Генератор чисел Фибоначчи работает путем ленивой генерации каждого следующего числа по мере запроса. В отличие от обычных методов, таких как рекурсивные или итеративные подходы, генератор создает только те числа, которые необходимы, и сразу же освобождает память после их использования.

Пример реализации генератора:

def fibonacci_generator():
a, b = 0, 1
while True:
yield a
a, b = b, a + b

Этот код создает бесконечную последовательность чисел Фибоначчи. Ключевая особенность заключается в использовании ключевого слова yield, которое позволяет приостановить выполнение функции и вернуть текущее значение, не теряя состояния между вызовами. В результате память используется более эффективно, так как все числа генерируются по мере необходимости.

Для вычисления суммы первых n чисел Фибоначчи можно воспользоваться следующим образом:

def sum_fibonacci(n):
fib_gen = fibonacci_generator()
return sum(next(fib_gen) for _ in range(n))

В этом примере генератор fibonacci_generator() создает последовательность чисел Фибоначчи, а функция sum_fibonacci() суммирует первые n элементов. Благодаря использованию генераторов, мы избегаем хранения всех значений в памяти, что особенно полезно при больших n.

Использование встроенных функций Python для ускорения вычислений

Пример использования reduce() из модуля functools позволяет эффективно вычислять последовательности чисел Фибоначчи за счет обработки данных без явных циклов. Преимущество reduce() заключается в том, что она выполняет операции с накоплением, что минимизирует количество промежуточных шагов.

Для ускорения работы с большими числами можно использовать lru_cache из того же модуля functools. Это декоратор, который сохраняет результаты вызовов функций с одинаковыми аргументами, что позволяет избежать повторных вычислений и ускоряет работу программы.

Если ваша задача состоит в вычислении суммы чисел Фибоначчи до заданного индекса, стоит использовать map(), который применяет функцию ко всем элементам в последовательности, что часто бывает быстрее, чем вручную прописанные циклы.

Ниже приведен пример использования lru_cache для оптимизации вычислений чисел Фибоначчи:

from functools import lru_cache
@lru_cache(maxsize=None)
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2)
sum_of_fib = sum(fibonacci(i) for i in range(10))
print(sum_of_fib)

Кроме того, можно воспользоваться функциями для работы с генераторами, такими как yield, чтобы избежать хранения всех значений в памяти, что будет полезно при больших числах Фибоначчи.

Для работы с большими объемами данных эффективным решением будет использование встроенной библиотеки itertools, которая предоставляет генераторы, оптимизированные для работы с большими наборами данных.

Преимущества и недостатки различных методов вычисления суммы чисел Фибоначчи

Итерация – оптимальный вариант при расчёте суммы до 10⁷ включительно. Работает стабильно, не требует дополнительной памяти, кроме счётчиков и накопителя суммы. Подходит для большинства прикладных задач. Недостаток – линейная сложность O(n), что делает метод непрактичным при очень больших n, например, выше 10⁸.

Рекурсия без мемоизации даёт слишком высокую стоимость выполнения. При n=40 количество вызовов превышает 200 тысяч, при n=50 – уже десятки миллионов. Использовать нецелесообразно даже для тестов. Мемоизация снижает нагрузку, но остаётся зависимость от размера кэша и необходимости хранения значений в памяти.

Формула суммы через F_n+2 − 1 показывает наилучший результат по скорости при использовании надёжного способа вычисления нужного члена. При n до 10⁹ и выше такой подход обрабатывается за миллисекунды. Уязвимость метода – необходимость точного и быстрого получения значения F_n+2, иначе выигрыш теряется. Наивный способ вычисления F_n+2 нивелирует преимущество формулы.

Матричное возведение в степень позволяет получать значение F_n за O(log n), что делает его пригодным при расчётах суммы по формуле. Хорошо работает на больших диапазонах, где линейные методы уже не справляются. Требует точной реализации и контроля переполнения при работе с большими числами. Для практики рекомендуется использовать целочисленную арифметику без округлений.

Тестирование и отладка функции для вычисления суммы чисел Фибоначчи

Для проверки корректности функции используйте фиксированные значения входного параметра. Например, при n = 5 сумма первых шести чисел Фибоначчи (0, 1, 1, 2, 3, 5) должна быть равна 12. При n = 0 результат – 0, при n = 1 – 1. Эти значения можно сравнить с ожидаемыми результатами в assert-выражениях:

assert fibonacci_sum(0) == 0
assert fibonacci_sum(1) == 1
assert fibonacci_sum(5) == 12
assert fibonacci_sum(10) == 143

Если используется рекурсивный подход, проверьте поведение на больших значениях n, например, n = 30. Рекурсивная реализация без мемоизации вызовет замедление или переполнение стека. Для таких случаев нужна итеративная реализация или кеширование через @lru_cache.

for i in range(n + 1):
print(f"i={i}, fib={fib}, total={total}")

Проверьте граничные случаи: отрицательные числа, тип входных данных. При передаче строки или None функция должна вызывать исключение. Добавьте обработку типа через isinstance и выбрасывание TypeError.

Для автоматизации тестов создайте набор unit-тестов с использованием модуля unittest. Это позволяет быстро проверять изменения в коде без ручной проверки каждого случая:

import unittest
class TestFibonacciSum(unittest.TestCase):
def test_small_values(self):
self.assertEqual(fibonacci_sum(0), 0)
self.assertEqual(fibonacci_sum(1), 1)
self.assertEqual(fibonacci_sum(5), 12)
def test_invalid_input(self):
with self.assertRaises(TypeError):
fibonacci_sum("10")

Проверяйте не только результат, но и скорость выполнения на больших значениях n. Если вычисление занимает заметное время, используйте профилировщик – модуль cProfile покажет узкие места.

Вопрос-ответ: